
科目: 来源: 题型:
【题目】如图所示,![]() 是一块边长为7米的正方形铁皮,其中
是一块边长为7米的正方形铁皮,其中![]() 是一半径为6米的扇形,已经被腐蚀不能使用,其余部分完好可利用.工人师傅想在未被腐蚀部分截下一个有边落在BC与CD上的长方形铁皮
是一半径为6米的扇形,已经被腐蚀不能使用,其余部分完好可利用.工人师傅想在未被腐蚀部分截下一个有边落在BC与CD上的长方形铁皮![]() ,其中P是
,其中P是![]() 上一点.设
上一点.设![]() ,长方形
,长方形![]() 的面积为S平方米.
的面积为S平方米.

(1)求S关于![]() 的函数解析式;
的函数解析式;
(2)设![]() ,求S关于t的表达式以及S的最大值.
,求S关于t的表达式以及S的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】当函数的自变量取值区间与值域区间相同时,我们称这样的区间为该函数的保值区间,函数的保值区间有![]() 、
、![]() 、
、![]() 三种形式,以下四个二次函数图像的对称轴是直线
三种形式,以下四个二次函数图像的对称轴是直线![]() ,从图像可知,有二个保值区间的函数是( )
,从图像可知,有二个保值区间的函数是( )
A.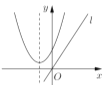 B.
B. C.
C.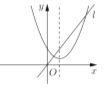 D.
D.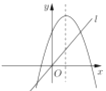
查看答案和解析>>
科目: 来源: 题型:
【题目】已知曲线C的极坐标方程是ρ=2cos θ,以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线l的参数方程是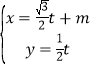 (t为参数).
(t为参数).
(1)求曲线C的直角坐标方程和直线l的普通方程;
(2)当m=2时,直线l与曲线C交于A、B两点,求|AB|的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知两个无穷数列![]() 分别满足
分别满足![]() ,
,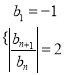 ,
,
其中![]() ,设数列
,设数列![]() 的前
的前![]() 项和分别为
项和分别为![]() ,
,
(1)若数列![]() 都为递增数列,求数列
都为递增数列,求数列![]() 的通项公式;
的通项公式;
(2)若数列![]() 满足:存在唯一的正整数
满足:存在唯一的正整数![]() (
(![]() ),使得
),使得![]() ,称数列
,称数列![]() 为“
为“![]() 坠点数列”
坠点数列”
①若数列![]() 为“5坠点数列”,求
为“5坠点数列”,求![]() ;
;
②若数列![]() 为“
为“![]() 坠点数列”,数列
坠点数列”,数列![]() 为“
为“![]() 坠点数列”,是否存在正整数
坠点数列”,是否存在正整数![]() ,使得
,使得![]() ,若存在,求
,若存在,求![]() 的最大值;若不存在,说明理由.
的最大值;若不存在,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】设十人各拿一只水桶,同到水龙头前打水,设水龙头注满第i(i=1,2,…,10)个人的水桶需Ti分钟,假设Ti各不相同,当水龙头只有一个可用时,应如何安排他(她)们的接水次序,使他(她)们的总的花费时间(包括等待时间和自己接水所花费的时间)最少( )
A. 从Ti中最大的开始,按由大到小的顺序排队
B. 从Ti中最小的开始,按由小到大的顺序排队
C. 从靠近Ti平均数的一个开始,依次按取一个小的取一个大的的摆动顺序排队
D. 任意顺序排队接水的总时间都不变
查看答案和解析>>
科目: 来源: 题型:
【题目】临近2020年春节,西宁市各卖场挖空心思寻找促销策略.商人张三丰善于运用数学思维进行销售分析,他根据以往当地的需求情况,得出如下他所经营的某种产品日需求量的频率分布直方图.
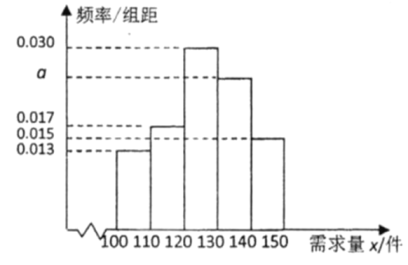
(1)求图中![]() 的值,并估计日需求量的众数:
的值,并估计日需求量的众数:
(2)某日,张三丰购进130件该种产品,根据近期市场行情,当天每售出1件能获利30元,未售出的部分,每件亏损20元设当天的需求量为![]() 件
件![]() ,纯利润为
,纯利润为![]() 元
元
(i)将![]() 表示为
表示为![]() 的函数;(ii)根据直方图估计当天纯利润
的函数;(ii)根据直方图估计当天纯利润![]() 不少于3400元的概率.
不少于3400元的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】对于定义在![]() 上的函数
上的函数![]() ,若同时满足:①存在闭区间
,若同时满足:①存在闭区间![]() ,使得任取
,使得任取![]() ,都有
,都有![]() (
(![]() 是常数);②对于
是常数);②对于![]() 内任意
内任意![]() ,当
,当![]() 时总有
时总有![]() ,称
,称![]() 为“平底型”函数.
为“平底型”函数.
(1)判断![]() ,
,![]() 是否为“平底型”函数?说明理由;
是否为“平底型”函数?说明理由;
(2)设![]() 是(1)中的“平底型”函数,若
是(1)中的“平底型”函数,若![]() 对一切
对一切![]() 恒成立,求实数
恒成立,求实数![]() 的范围;
的范围;
(3)若![]() ,
,![]() 是“平底型”函数,求
是“平底型”函数,求![]() 和
和![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知动点P到定点![]() 的距离与点P到定直线
的距离与点P到定直线![]() 的距离之比为
的距离之比为![]()
(1)求动点P的轨迹C的方程;
(2)设M、N是直线l上的两个点,点E是点F关于原点的对称点,若![]() ,求 | MN | 的最小值.
,求 | MN | 的最小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() 和直线
和直线![]() :
: ![]() ,椭圆的离心率
,椭圆的离心率![]() ,坐标原点到直线
,坐标原点到直线![]() 的距离为
的距离为![]() .
.
(Ⅰ)求椭圆的方程;
(Ⅱ)已知定点![]() ,若直线
,若直线![]() 过点
过点![]() 且与椭圆相交于
且与椭圆相交于![]() 两点,试判断是否存在直线
两点,试判断是否存在直线![]() ,使以
,使以![]() 为直径的圆过点
为直径的圆过点![]() ?若存在,求出直线
?若存在,求出直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com