
科目: 来源: 题型:
【题目】为了保障全国第四次经济普查顺利进行,国家统计局从东部选择江苏, 从中部选择河北. 湖北,从西部选择宁夏, 从直辖市中选择重庆作为国家综合试点地区,然后再逐级确定普查区域,直到基层的普查小区.在普查过程中首先要进行宣传培训,然后确定对象,最后入户登记. 由于种种情况可能会导致入户登记不够顺利,这为正式普查提供了宝贵的试点经验. 在某普查小区,共有 50 家企事业单位,150 家个体经营户,普查情况如下表所示:
普查对象类别 | 顺利 | 不顺利 | 合计 |
企事业单位 | 40 | 10 | 50 |
个体经营户 | 100 | 50 | 150 |
合计 | 140 | 60 | 200 |
(1)写出选择 5 个国家综合试点地区采用的抽样方法;
(2)根据列联表判断是否有![]() 的把握认为“此普查小区的入户登记是否顺利与普查对象的类别有关”;
的把握认为“此普查小区的入户登记是否顺利与普查对象的类别有关”;
(3)以频率作为概率, 某普查小组从该小区随机选择 1 家企事业单位,3 家个体经营户作为普查对象,入户登记顺利的对象数记为![]() , 写出
, 写出![]() 的分布列,并求
的分布列,并求![]() 的期望值.
的期望值.
附:![]()
| 0.10 | 0.010 | 0.001 |
| 2.706 | 6.635 | 10.828 |
查看答案和解析>>
科目: 来源: 题型:
【题目】在中国,不仅是购物,而且从共享单车到医院挂号再到公共缴费,日常生活中几乎全部领域都支持手机支付.出门不带现金的人数正在迅速增加。中国人民大学和法国调查公司益普索合作,调查了腾讯服务的6000名用户,从中随机抽取了60名,统计他们出门随身携带现金(单位:元)如茎叶图如示,规定:随身携带的现金在100元以下(不含100元)的为“手机支付族”,其他为“非手机支付族”.

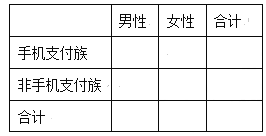
(1)根据上述样本数据,将![]() 列联表补充完整,并判断有多大的把握认为“手机支付族”与“性别”有关?
列联表补充完整,并判断有多大的把握认为“手机支付族”与“性别”有关?
(2)用样本估计总体,若从腾讯服务的用户中随机抽取3位女性用户,这3位用户中“手机支付族”的人数为![]() ,求随机变量
,求随机变量![]() 的期望和方差;
的期望和方差;
(3)某商场为了推广手机支付,特推出两种优惠方案,方案一:手机支付消费每满1000元可直减100元;方案二:手机支付消费每满1000元可抽奖2次,每次中奖的概率同为![]() ,且每次抽奖互不影响,中奖一次打9折,中奖两次打8.5折.如果你打算用手机支付购买某样价值1200元的商品,请从实际付款金额的数学期望的角度分析,选择哪种优惠方案更划算?
,且每次抽奖互不影响,中奖一次打9折,中奖两次打8.5折.如果你打算用手机支付购买某样价值1200元的商品,请从实际付款金额的数学期望的角度分析,选择哪种优惠方案更划算?
附:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
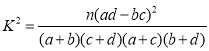
查看答案和解析>>
科目: 来源: 题型:
【题目】十九大以来,国家深入推进精准脱贫,加大资金投入,强化社会帮扶,为了更好的服务于人民,派调查组到某农村去考察和指导工作.该地区有100户农民,且都从事水果种植,据了解,平均每户的年收入为2万元.为了调整产业结构,调查组和当地政府决定动员部分农民从事水果加工,据估计,若能动员![]() 户农民从事水果加工,则剩下的继续从事水果种植的农民平均每户的年收入有望提高
户农民从事水果加工,则剩下的继续从事水果种植的农民平均每户的年收入有望提高![]() ,而从事水果加工的农民平均每户收入将为
,而从事水果加工的农民平均每户收入将为![]() 万元.
万元.
(1)若动员![]() 户农民从事水果加工后,要使从事水果种植的农民的总年收入不低于动员前从事水果种植的农民的总年收入,求
户农民从事水果加工后,要使从事水果种植的农民的总年收入不低于动员前从事水果种植的农民的总年收入,求![]() 的取值范围;
的取值范围;
(2)在(1)的条件下,要使这100户农民中从事水果加工的农民的总收入始终不高于从事水果种植的农民的总收入,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】在正方体![]() 中,已知点
中,已知点![]() 在直线
在直线![]() 上运动,则下列四个命题中:①三棱锥
上运动,则下列四个命题中:①三棱锥![]() 的体积不变;②
的体积不变;②![]() ;③当
;③当![]() 为
为![]() 中点时,二面角
中点时,二面角![]() 的余弦值为
的余弦值为![]() ;④若正方体的棱长为2,则
;④若正方体的棱长为2,则![]() 的最小值为
的最小值为![]() ;其中说法正确的是____________(写出所有说法正确的编号)
;其中说法正确的是____________(写出所有说法正确的编号)
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() 是定义在R上的偶函数,且当
是定义在R上的偶函数,且当![]() 时,
时,![]() (
(![]() ).
).
(1)当![]() 时,求
时,求![]() 的表达式:
的表达式:
(2)求![]() 在区间
在区间![]() 的最大值
的最大值![]() 的表达式;
的表达式;
(3)当![]() 时,若关于x的方程
时,若关于x的方程![]() (a,
(a,![]() )恰有10个不同实数解,求a的取值范围.
)恰有10个不同实数解,求a的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】以下四个命题:①两个随机变量的线性相关性越强,相关系数的绝对值越接近1;②在回归分析中,可用相关指数![]() 的值判断拟合效果,
的值判断拟合效果,![]() 越小,模型的拟合效果越好; ③若数据
越小,模型的拟合效果越好; ③若数据![]() 的方差为1,则
的方差为1,则![]() 的方差为4;④已知一组具有线性相关关系的数据
的方差为4;④已知一组具有线性相关关系的数据![]() ,其线性回归方程
,其线性回归方程![]() ,则“
,则“![]() 满足线性回归方程
满足线性回归方程![]() ”是“
”是“![]() ,
,![]() ”的充要条件;其中真命题的个数为( )
”的充要条件;其中真命题的个数为( )
A.4B.3C.2D.1
查看答案和解析>>
科目: 来源: 题型:
【题目】某大学生在开学季准备销售一种文具套盒进行试创业,在一个开学季内,每售出1盒该产品获利50元,未售出的产品,每盒亏损30元.根据历史资料,得到开学季市场需求量的频率分布直方图,如图所示.该同学为这个开学季进了160盒该产品,以![]() (单位:盒,
(单位:盒,![]() )表示这个开学季内的市场需求量,
)表示这个开学季内的市场需求量,![]() (单位:元)表示这个开学季内经销该产品的利润.
(单位:元)表示这个开学季内经销该产品的利润.
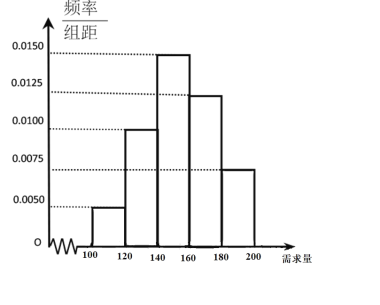
(1)根据直方图估计这个开学季内市场需求量![]() 的平均数和众数;
的平均数和众数;
(2)将![]() 表示为
表示为![]() 的函数;
的函数;
(3)以需求量的频率作为各需求量的概率,求开学季利润不少于4800元的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】学校艺术节对![]() 四件参赛作品只评一件一等奖,在评奖揭晓前,甲,乙,丙,丁四位同学对这四件参赛作品预测如下:
四件参赛作品只评一件一等奖,在评奖揭晓前,甲,乙,丙,丁四位同学对这四件参赛作品预测如下:
甲说:“是![]() 或
或![]() 作品获得一等奖”; 乙说:“
作品获得一等奖”; 乙说:“ ![]() 作品获得一等奖”;
作品获得一等奖”;
丙说:“ ![]() 两件作品未获得一等奖”; 丁说:“是
两件作品未获得一等奖”; 丁说:“是![]() 作品获得一等奖”.
作品获得一等奖”.
评奖揭晓后,发现这四位同学中只有两位说的话是对的,则获得一等奖的作品是_________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com