（1）求这500名患者潜伏期的平均数（同一组中的数据用该组区间的中点值作代表），并计算出这500名患者中“长潜伏者”的人数；

（2）为研究潜伏期与患者年龄的关系，以潜伏期是否高于平均数为标准进行分层抽样，从上述500名患者中抽取300人，得到如下表格.

（i）请将表格补充完整；

（ii）研究发现，某药物对新冠病毒有一定的抑制作用，现需在样本中60岁以下的140名患者中按分层抽样方法抽取7人做I期临床试验，再从选取的7人中随机抽取两人做Ⅱ期临床试验，求两人中恰有1人为“长潜伏者”的概率.

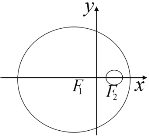
【题目】如图，已知圆的方程为，圆的方程为，若动圆与圆内切，与圆外切．

（Ⅰ）求动圆圆心的轨迹的方程；

（Ⅱ）过直线上的点作圆的两条切线，设切点分别是，，若直线与轨迹交于，两点，求的最小值．

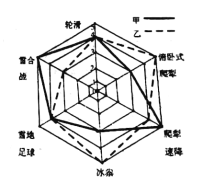
A.甲的轮滑指标高于他的雪地足球指标

B.乙的雪地足球指标低于甲的冰尜指标

C.甲的爬犁速降指标高于乙的爬犁速降指标

D.乙的俯卧式爬犁指标低于甲的雪合战指标

【题目】已知函数．

（1）当时，求函数在点处的切线方程．

（2）若对任意的恒成立，求的值．

（3）在（2）的条件下，记，证明：存在唯一的极大值点，且．

【题目】某公司为确定下一年度投入某种产品的宣传费，需了解年宣传费（单位：万元）对年销售量（单位：吨）和年利润（单位：万元）的影响．对近六年的年宣传费和年销售量（）的数据作了初步统计，得到如下数据：

经电脑模拟，发现年宣传费（万元）与年销售量（吨）之间近似满足关系式（）．对上述数据作了初步处理，得到相关的值如表：

（1）根据所给数据，求关于的回归方程；

（2）已知这种产品的年利润与，的关系为若想在年达到年利润最大，请预测年的宣传费用是多少万元？

附：对于一组数据，，…，，其回归直线中的斜率和截距的最小二乘估计分别为，

【题目】已知是实数，函数．

（1）当时，求函数的单调区间及极值；

（2）设为在区间上的最小值，写出的表达式．

【题目】如图，四棱锥P一ABCD中，AB=AD=2BC=2，BC∥AD，AB⊥AD，△PBD为正三角形．且PA=2．

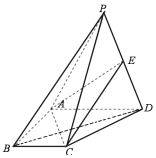
（1）证明：平面PAB⊥平面PBC；

（2）若点P到底面ABCD的距离为2，E是线段PD上一点，且PB∥平面ACE，求四面体A-CDE的体积．

【题目】已知函数，若函数在上有两个不同的零点，则实数的取值范围是__________．

【题目】如图，已知抛物线 ，直线与抛物线相交于两点，且当倾斜角为的直线经过抛物线的焦点时，有.

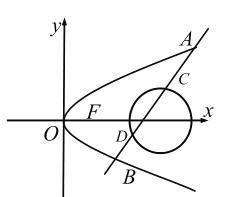
（1）求抛物线的方程；

（2）已知圆，是否存在倾斜角不为的直线，使得线段被圆截成三等分？若存在，求出直线的方程；若不存在，请说明理由.

【题目】癌症是迄今为止人类尚未攻克的疾病之一，目前，癌症只能尽量预防．某医学中心推出了一种抗癌症的制剂，现对20位癌症病人，进行医学试验测试药效，测试结果分为“病人死亡”和“病人存活”，现对测试结果和药物剂量（单位：）进行统计，规定病人在服用（包括）以上为“足量”，否则为“不足量”，统计结果显示，这20病人

中“病人存活”的有13位，对病人服用的药物剂量统计如下表：

已知“病人存活”，但服用的药物剂量不足的病人共1位．

（1）完成下列列联表，并判断是否可以在犯错误的概率不超过1%的前提下，认为“病人存活”与服用药物的剂量足量有关？

（2）若在该样本“服用药物剂量不足”的病人中随机抽取3位，求这三人中恰有1位“病人存活”的概率．

参考数据: