【题目】设命题：实数满足不等式；命题：函数 有极值点.

（1）若为真命题，为假命题，求实数的取值范围；

（2）若为真命题，并记为，且，若是的必要不充分条件，求实数的取值范围.

【题目】已知函数.

（1）求在点处的切线方程；

（2）若方程有两个实数根，，且，证明.

【题目】如图，是由两个全等的菱形和组成的空间图形，，∠BAF＝∠ECD＝60°.

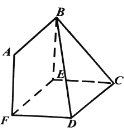
（1）求证：；

（2）如果二面角B－EF－D的平面角为60°，求直线与平面所成角的正弦值.

【题目】如图，多面体中，四边形为矩形，二面角为，，，，，.

（1）求证：平面；

（2）为线段上的点，当时，求二面角的余弦值.

【题目】椭圆的左、右焦点分别为，右顶点为A，上顶点为B，且满足向量 。

（1）若，求椭圆的标准方程;

（2）设为椭圆上异于顶点的点，以线段PB为直径的圆经过F1，问是否存在过F2的直线与该圆相切？若存在，求出其斜率；若不存在，说明理由。

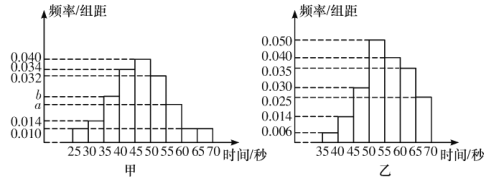
（1）若甲解开密码锁所需时间的中位数为47，求、的值，并分别求出甲、乙在1分钟内解开密码锁的频率；

（2）若以解开密码锁所需时间位于各区间的频率代替解开密码锁所需时间位于该区间的概率，并且丙在1分钟内解开密码锁的概率为0.5，各人是否解开密码锁相互独立.

①按乙丙甲的先后顺序和按丙乙甲的先后顺序哪一种可使派出人员数目的数学期望更小.

②试猜想：该团队以怎样的先后顺序派出人员，可使所需派出的人员数目的数学期望达到最小，不需要说明理由.

【题目】已知函数，对任意，都有.

讨论的单调性；

当存在三个不同的零点时，求实数的取值范围.

【题目】在直角坐标系中中，曲线的参数方程为（为参数，）.以坐标原点为极点，轴正半轴为极轴建立极坐标系，已知直线的极坐标方程为.

（1）设是曲线上的一个动点，当时，求点到直线的距离的最大值；

（2）若曲线上所有的点均在直线的右下方，求的取值范围.

【题目】数学老师给出一个函数，甲、乙、丙、丁四个同学各说出了这个函数的一条性质：甲：在 上函数单调递减；乙：在上函数单调递增；丙：在定义域R上函数的图象关于直线对称；丁：不是函数的最小值．老师说：你们四个同学中恰好有三个人说的正确．那么，你认为____说的是错误的．

【题目】在棱长为2的正方体中，点M是对角线上的点（点M与A、不重合），则下列结论正确的个数为（ ）

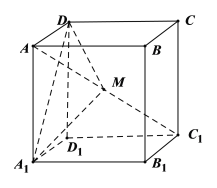
①存在点M，使得平面平面；

②存在点M，使得平面；

③若的面积为S，则；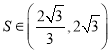

④若、分别是在平面与平面的正投影的面积，则存在点M，使得.

A.1个B.2个C.3个D.4个