
科目: 来源: 题型:
【题目】“割圆术”是我国古代计算圆周率![]() 的一种方法.在公元
的一种方法.在公元![]() 年左右,由魏晋时期的数学家刘徽发明.其原理就是利用圆内接正多边形的面积逐步逼近圆的面积,进而求
年左右,由魏晋时期的数学家刘徽发明.其原理就是利用圆内接正多边形的面积逐步逼近圆的面积,进而求![]() .当时刘微就是利用这种方法,把
.当时刘微就是利用这种方法,把![]() 的近似值计算到
的近似值计算到![]() 和
和![]() 之间,这是当时世界上对圆周率
之间,这是当时世界上对圆周率![]() 的计算最精确的数据.这种方法的可贵之处就是利用已知的、可求的来逼近未知的、要求的,用有限的来逼近无穷的.为此,刘微把它概括为“割之弥细,所失弥少,割之又割,以至于不可割,则与圆合体,而无所失矣”.这种方法极其重要,对后世产生了巨大影响,在欧洲,这种方法后来就演变为现在的微积分.根据“割圆术”,若用正二十四边形来估算圆周率
的计算最精确的数据.这种方法的可贵之处就是利用已知的、可求的来逼近未知的、要求的,用有限的来逼近无穷的.为此,刘微把它概括为“割之弥细,所失弥少,割之又割,以至于不可割,则与圆合体,而无所失矣”.这种方法极其重要,对后世产生了巨大影响,在欧洲,这种方法后来就演变为现在的微积分.根据“割圆术”,若用正二十四边形来估算圆周率![]() ,则
,则![]() 的近似值是( )(精确到
的近似值是( )(精确到![]() )(参考数据
)(参考数据![]() )
)

A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线l:
中,直线l:![]() ,以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线
,以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线![]() .
.
(Ⅰ)求曲线C被直线l截得的弦长;
(Ⅱ)与直线l垂直的直线EF与曲线C相切于点Q,求点Q的直角坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】春季气温逐渐攀升,病菌滋生传播快,为了确保安全开学,学校按30名学生一批,组织学生进行某种传染病毒的筛查,学生先到医务室进行血检,检呈阳性者需到防疫部门]做进一步检测.学校综合考虑了组织管理、医学检验能力等多万面的因素,根据经验,采用分组检测法可有效减少工作量,具体操作如下:将待检学生随机等分成若干组,先将每组的血样混在一起化验,若结果呈阴性,则可断定本组血样合格,不必再做进一步的检测;若结果呈阳性,则本组中的每名学生再逐个进行检测.现有两个分组方案:方案一:将30人分成5组,每组6人;方案二:将30人分成6组,每组5人.已知随机抽一人血检呈阳性的概率为0.5%,且每个人血检是否呈阳性相互独立.
(Ⅰ)请帮学校计算一下哪一个分组方案的工作量较少?
(Ⅱ)已知该传染疾病的患病率为0.45%,且患该传染疾病者血检呈阳性的概率为99.9%,若检测中有一人血检呈阳性,求其确实患该传染疾病的概率.(参考数据:(![]() ,
,![]() )
)
查看答案和解析>>
科目: 来源: 题型:
【题目】已知抛物线C:![]() 的焦点为F,Q是抛物线上的一点,
的焦点为F,Q是抛物线上的一点,![]() .
.
(Ⅰ)求抛物线C的方程;
(Ⅱ)过点![]() 作直线l与抛物线C交于M,N两点,在x轴上是否存在一点A,使得x轴平分
作直线l与抛物线C交于M,N两点,在x轴上是否存在一点A,使得x轴平分![]() ?若存在,求出点A的坐标,若不存在,请说明理由.
?若存在,求出点A的坐标,若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
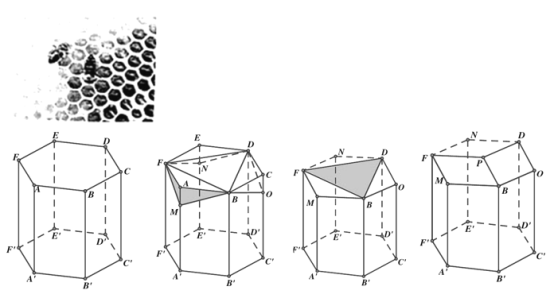
【题目】蜂巢是由工蜂分泌蜂蜡建成的从正面看,蜂巢口是由许多正六边形的中空柱状体连接而成,中空柱状体的底部是由三个全等的菱形面构成,菱形的一个角度是![]() ,这样的设计含有深刻的数学原理、我国著名数学家华罗庚曾专门研究蜂巢的结构著有《谈谈与蜂房结构有关的数学问题》.用数学的眼光去看蜂巢的结构,如图,在六棱柱
,这样的设计含有深刻的数学原理、我国著名数学家华罗庚曾专门研究蜂巢的结构著有《谈谈与蜂房结构有关的数学问题》.用数学的眼光去看蜂巢的结构,如图,在六棱柱![]() 的三个顶点A,C,E处分别用平面BFM,平面BDO,平面DFN截掉三个相等的三棱锥
的三个顶点A,C,E处分别用平面BFM,平面BDO,平面DFN截掉三个相等的三棱锥![]() ,
,![]() ,
,![]() ,平面BFM,平面BDO,平面DFN交于点P,就形成了蜂巢的结构.如图,设平面PBOD与正六边形底面所成的二面角的大小为
,平面BFM,平面BDO,平面DFN交于点P,就形成了蜂巢的结构.如图,设平面PBOD与正六边形底面所成的二面角的大小为![]() ,则有:( )
,则有:( )
A.![]() B.
B.![]()
C.![]() D.以上都不对
D.以上都不对
查看答案和解析>>
科目: 来源: 题型:
【题目】函数![]() (
(![]() ,
,![]() )的部分图象如图中实线所示,图中圆C与
)的部分图象如图中实线所示,图中圆C与![]() 的图象交于M,N两点,且M在y轴上,则下列说法中正确的是( )
的图象交于M,N两点,且M在y轴上,则下列说法中正确的是( )

A.函数![]() 的最小正周期是2π
的最小正周期是2π
B.函数![]() 的图象关于点
的图象关于点![]() 成中心对称
成中心对称
C.函数![]() 在
在![]() 单调递增
单调递增
D.将函数![]() 的图象向左平移
的图象向左平移![]() 后得到的关于y轴对称
后得到的关于y轴对称
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() ,以坐标原点
,以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() .
.
(Ⅰ)求曲线![]() 被直线
被直线![]() 截得的弦长;
截得的弦长;
(Ⅱ)与直线![]() 垂直的直线
垂直的直线![]() 与曲线
与曲线![]() 相切于点
相切于点![]() ,求点
,求点![]() 的直角坐标.
的直角坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】某传染病疫情爆发期间,当地政府积极整合医疗资源,建立“舱医院”对所有密切接触者进行14天的隔离观察治疗.治疗期满后若检测指标仍未达到合格标准,则转入指定专科医院做进一步的治疗.“舱医院”对所有人员在“入口”及“出口”时都进行了医学指标检测,若“入口”检测指标在35以下者则不需进入“舱医院”而是直接进入指定专科医院进行治疗.以下是20名进入“舱医院”的密切接触者的“入口”及“出口”医学检测指标:
入口 | 50 | 35 | 35 | 40 | 55 | 90 | 80 | 60 | 60 | 60 | 65 | 35 | 60 | 90 | 35 | 40 | 55 | 50 | 65 | 50 |
出口 | 70 | 50 | 60 | 50 | 75 | 70 | 85 | 70 | 80 | 70 | 55 | 50 | 75 | 90 | 60 | 60 | 65 | 70 | 75 | 70 |
(Ⅰ)建立![]() 关于
关于![]() 的回归方程;(回归方程的系数精确到0.1)
的回归方程;(回归方程的系数精确到0.1)
(Ⅱ)如果60是“舱医院”的“出口”最低合格指标,那么,“入口”指标低于多少时,将来这些密切接触者将不能进入“舱医院”而是直接进入指定专科医院接受治疗.(检测指标为整数)
附注:参考数据:![]() ,
,![]() .
.
参考公式:回归方程![]() 中斜率和截距的最小二乘法估计公式分别为:
中斜率和截距的最小二乘法估计公式分别为: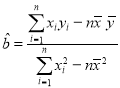 ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com