
科目: 来源: 题型:
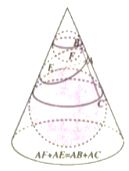
【题目】如图所示,在顶角为![]() 圆锥内有一截面,在圆锥内放半径分别为
圆锥内有一截面,在圆锥内放半径分别为![]() 的两个球与圆锥的侧面、截面相切,两个球分别与截面相切于
的两个球与圆锥的侧面、截面相切,两个球分别与截面相切于![]() ,则截面所表示的椭圆的离心率为( )
,则截面所表示的椭圆的离心率为( )
(注:在截口曲线上任取一点![]() ,过
,过![]() 作圆锥的母线,分别与两个球相切于点
作圆锥的母线,分别与两个球相切于点![]() ,由相切的几何性质可知,
,由相切的几何性质可知,![]() ,
,![]() ,于是
,于是![]() ,为椭圆的几何意义)
,为椭圆的几何意义)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() 的左焦点为F,点
的左焦点为F,点![]() ,过M的直线与椭圆E交于A,B两点,线段AB中点为C,设椭圆E在A,B两点处的切线相交于点P,O为坐标原点.
,过M的直线与椭圆E交于A,B两点,线段AB中点为C,设椭圆E在A,B两点处的切线相交于点P,O为坐标原点.
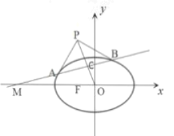
(1)证明:O、C、P三点共线;
(2)已知![]() 是抛物线
是抛物线![]() 的弦,所在直线过该抛物线的准线与y轴的交点,
的弦,所在直线过该抛物线的准线与y轴的交点,![]() 是弦
是弦![]() 在两端点处的切线的交点,小明同学猜想:
在两端点处的切线的交点,小明同学猜想:![]() 在定直线上.你认为小明猜想合理吗?若合理,请写出
在定直线上.你认为小明猜想合理吗?若合理,请写出![]() 所在直线方程;若不合理,请说明理由.
所在直线方程;若不合理,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】某学校为进一步规范校园管理,强化饮食安全,提出了“远离外卖,健康饮食”的口号.当然,也需要学校食堂能提供安全丰富的菜品来满足同学们的需求.在学期末,校学生会为了调研学生对本校食堂A部和B部的用餐满意度,从在A部和B部都用过餐的学生中随机抽取了200人,每人分别对其评分,满分为100分.随后整理评分数据,将分数分成6组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() ,第6组
,第6组![]() ,得到A部分数的频率分布直方图和B部分数的频数分布表.
,得到A部分数的频率分布直方图和B部分数的频数分布表.

分数区间 | 频数 |
| 7 |
| 18 |
| 21 |
| 24 |
| 70 |
| 60 |
定义:学生对食堂的“满意度指数”
分数 |
|
|
|
|
|
|
满意度指数 | 0 | 1 | 2 | 3 | 4 | 5 |
(1)求A部得分的中位数(精确到小数点后一位);
(2)A部为进一步改善经营,从打分在80分以下的前四组中,采用分层抽样的方法抽取8人进行座谈,再从这8人中随机抽取3人参与“端午节包粽子”实践活动,在第3组抽到1人的情况下,第4组抽到2人的概率;
(3)如果根据调研结果评选学生放心餐厅,应该评选A部还是B部(将频率视为概率)
查看答案和解析>>
科目: 来源: 题型:
【题目】在平行四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 是EA的中点(如图1),将
是EA的中点(如图1),将![]() 沿CD折起到图2中
沿CD折起到图2中![]() 的位置,得到四棱锥是
的位置,得到四棱锥是![]() .
.
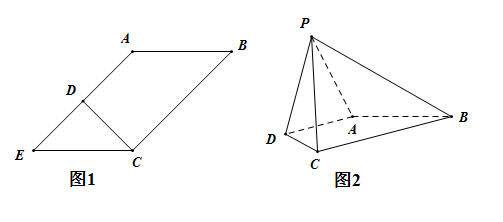
(1)求证:![]() 平面PDA;
平面PDA;
(2)若PD与平面ABCD所成的角为![]() .且
.且![]() 为锐角三角形,求平面PAD和平面PBC所成锐二面角的余弦值.
为锐角三角形,求平面PAD和平面PBC所成锐二面角的余弦值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知正方体![]() 的棱长为1,P是空间中任意一点,下列正确命题的个数是( )
的棱长为1,P是空间中任意一点,下列正确命题的个数是( )
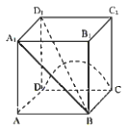
①若P为棱![]() 中点,则异面直线AP与CD所成角的正切值为
中点,则异面直线AP与CD所成角的正切值为![]() ;
;
②若P在线段![]() 上运动,则
上运动,则![]() 的最小值为
的最小值为![]() ;
;
③若P在半圆弧CD上运动,当三棱锥![]() 的体积最大时,三棱锥
的体积最大时,三棱锥![]() 外接球的表面积为
外接球的表面积为![]() ;
;
④若过点P的平面![]() 与正方体每条棱所成角相等,则
与正方体每条棱所成角相等,则![]() 截此正方体所得截面面积的最大值为
截此正方体所得截面面积的最大值为![]()
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目: 来源: 题型:
【题目】2019冠状病毒病(CoronaVirus Disease2019(COVID-19))是由新型冠状病毒(2019-nCoV)引发的疾病,目前全球感染者以百万计,我国在党中央、国务院、中央军委的坚强领导下,已经率先控制住疫情,但目前疫情防控形势依然严峻,湖北省中小学依然延期开学,所有学生按照停课不停学的要求,居家学习.小李同学在居家学习期间,从网上购买了一套高考数学冲刺模拟试卷,快递员计划在下午4:00~5:00之间送货到小区门口的快递柜中,小李同学父亲参加防疫志愿服务,按规定,他换班回家的时间在下午4:30~5:00,则小李父亲收到试卷无需等待的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() 的左焦点为F,点
的左焦点为F,点![]() ,过M的直线与椭圆E交于A,B两点,线段AB中点为C,设椭圆E在A,B两点处的切线相交于点P,O为坐标原点.
,过M的直线与椭圆E交于A,B两点,线段AB中点为C,设椭圆E在A,B两点处的切线相交于点P,O为坐标原点.
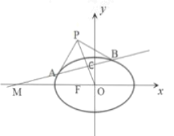
(1)证明:O、C、P三点共线;
(2)已知![]() 是抛物线
是抛物线![]() 的弦,所在直线过该抛物线的准线与y轴的交点,
的弦,所在直线过该抛物线的准线与y轴的交点,![]() 是弦
是弦![]() 在两端点处的切线的交点,小明同学猜想:
在两端点处的切线的交点,小明同学猜想:![]() 在定直线上.你认为小明猜想合理吗?若合理,请写出
在定直线上.你认为小明猜想合理吗?若合理,请写出![]() 所在直线方程;若不合理,请说明理由.
所在直线方程;若不合理,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】某学校为进一步规范校园管理,强化饮食安全,提出了“远离外卖,健康饮食”的口号.当然,也需要学校食堂能提供安全丰富的菜品来满足同学们的需求.在学期末,校学生会为了调研学生对本校食堂A部和B部的用餐满意度,从在A部和B部都用过餐的学生中随机抽取了200人,每人分别对其评分,满分为100分.随后整理评分数据,将分数分成6组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() ,第6组
,第6组![]() ,得到A部分数的频率分布直方图和B部分数的频数分布表.
,得到A部分数的频率分布直方图和B部分数的频数分布表.
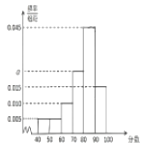
分数区间 | 频数 |
| 7 |
| 18 |
| 21 |
| 24 |
| 70 |
| 60 |
定义:学生对食堂的“满意度指数”
分数 |
|
|
|
|
|
|
满意度指数 | 0 | 1 | 2 | 3 | 4 | 5 |
(1)求A部得分的中位数(精确到小数点后一位);
(2)A部为进一步改善经营,从打分在80分以下的前四组中,采用分层抽样的方法抽取8人进行座谈,再从这8人中随机抽取3人参与“端午节包粽子”实践活动,在第3组抽到1人的情况下,第4组抽到2人的概率;
(3)如果根据调研结果评选学生放心餐厅,应该评选A部还是B部(将频率视为概率)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com