
科目: 来源: 题型:
【题目】对于定义在![]() 上的函数
上的函数![]() ,若函数
,若函数![]() 满足:①在区间
满足:①在区间![]() 上单调递减,②存在常数
上单调递减,②存在常数![]() ,使其值域为
,使其值域为![]() ,则称函数
,则称函数![]() 是函数
是函数![]() 的“渐近函数”.
的“渐近函数”.
(1)判断函数![]() 是不是函数
是不是函数![]() 的“渐近函数”,说明理由;
的“渐近函数”,说明理由;
(2)求证:函数![]() 不是函数
不是函数![]() 的“渐近函数”;
的“渐近函数”;
(3)若函数![]() ,
,![]() ,求证:当且仅当
,求证:当且仅当![]() 时,
时,![]() 是
是![]() 的“渐近函数”.
的“渐近函数”.
查看答案和解析>>
科目: 来源: 题型:
【题目】某市2013年发放汽车牌照12万张,其中燃油型汽车牌照10万张,电动型汽车2万张,为了节能减排和控制总量,从2013年开始,每年电动型汽车牌照按50%增长,而燃油型汽车牌照每一年比上一年减少0.5万张,同时规定一旦某年发放的牌照超过15万张,以后每一年发放的电动车的牌照的数量维持在这一年的水平不变.
(1)记2013年为第一年,每年发放的燃油型汽车牌照数量构成数列![]() ,每年发放电动型汽车牌照数为构成数列
,每年发放电动型汽车牌照数为构成数列![]() ,完成下列表格,并写出这两个数列的通项公式;
,完成下列表格,并写出这两个数列的通项公式;
(2)从2013年算起,累计各年发放的牌照数,哪一年开始超过200万张?
|
|
|
| |
|
|
|
|
查看答案和解析>>
科目: 来源: 题型:
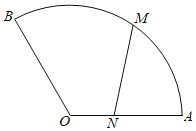
【题目】某公园草坪上有一扇形小径(如图),扇形半径为![]() ,中心角为
,中心角为![]() ,甲由扇形中心
,甲由扇形中心![]() 出发沿
出发沿![]() 以每秒2米的速度向
以每秒2米的速度向![]() 快走,同时乙从
快走,同时乙从![]() 出发,沿扇形弧以每秒
出发,沿扇形弧以每秒![]() 米的速度向
米的速度向![]() 慢跑,记
慢跑,记![]() 秒时甲、乙两人所在位置分别为
秒时甲、乙两人所在位置分别为![]() ,
,![]() ,通过计算
,通过计算![]() ,判断下列说法是否正确:
,判断下列说法是否正确:
(1)当![]() 时,函数
时,函数![]() 取最小值;
取最小值;
(2)函数![]() 在区间
在区间![]() 上是增函数;
上是增函数;
(3)若![]() 最小,则
最小,则![]() ;
;
(4)![]() 在
在![]() 上至少有两个零点;
上至少有两个零点;
其中正确的判断序号是______(把你认为正确的判断序号都填上)
查看答案和解析>>
科目: 来源: 题型:
【题目】记无穷数列![]() 的前
的前![]() 项中最大值为
项中最大值为![]() ,最小值为
,最小值为![]() ,令
,令![]()
(Ⅰ)若![]() ,请写出
,请写出![]() 的值;
的值;
(Ⅱ)求证:“数列![]() 是等差数列”是“数列
是等差数列”是“数列![]() 是等差数列”的充要条件;
是等差数列”的充要条件;
(Ⅲ)若![]() ,求证:存在
,求证:存在![]() ,使得
,使得![]() ,有
,有![]()
![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】已知抛物线![]() 的顶点为原点,其焦点
的顶点为原点,其焦点![]() 到直线
到直线![]() 的距离为
的距离为![]() .设
.设![]() 为直线
为直线![]() 上的点,过点
上的点,过点![]() 作抛物线
作抛物线![]() 的两条切线
的两条切线![]() ,其中
,其中![]() 为切点.
为切点.
(1) 求抛物线![]() 的方程;
的方程;
(2) 当点![]() 为直线
为直线![]() 上的定点时,求直线
上的定点时,求直线![]() 的方程;
的方程;
(3) 当点![]() 在直线
在直线![]() 上移动时,求
上移动时,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】若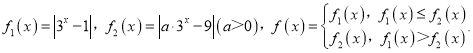
(1)当![]() 时,设
时,设![]() 所对应的自变量取值区间的长度为
所对应的自变量取值区间的长度为![]() (闭区间
(闭区间![]() 的长度为
的长度为![]() ),试求
),试求![]() 的最大值;
的最大值;
(2)是否存在这样的![]() 使得当
使得当![]() 时,
时,![]() ?若存在,求出
?若存在,求出![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】贺先生想向银行贷款买辆新能源车,银行可以贷给贺先生N元,一年后需要一次性还1.02N元.
(1)贺先生发现一个投资理财方案:每个月月初投资![]() 元,共投资一年,每月的月收益率达到1%,于是贺先生决定贷款12
元,共投资一年,每月的月收益率达到1%,于是贺先生决定贷款12![]() 元,按投资方案投资,求
元,按投资方案投资,求![]() 的值,使得贺先生用最终投所得的钱还清贷款后,还有120000的余额去旅游(精确到0.01元);
的值,使得贺先生用最终投所得的钱还清贷款后,还有120000的余额去旅游(精确到0.01元);
(2)贺先生又发现一个投资方案:第![]() 个月月初投资
个月月初投资![]() 元
元![]() 共投资一年,每月的月收益率达到1%,则贺先生应贷款多少,使得用最终投资所得的钱还清后,还有120000的余额去旅游(精确到0.01元).
共投资一年,每月的月收益率达到1%,则贺先生应贷款多少,使得用最终投资所得的钱还清后,还有120000的余额去旅游(精确到0.01元).
(参考数据![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目: 来源: 题型:
【题目】对于定义在![]() 上的函数
上的函数![]() ,如果存在两条平行直线
,如果存在两条平行直线![]() 与
与![]()
![]() ,使得对于任意
,使得对于任意![]() ,都有
,都有![]() 恒成立,那么称函数
恒成立,那么称函数![]() 是带状函数,若
是带状函数,若![]() ,
,![]() 之间的最小距离
之间的最小距离![]() 存在,则称
存在,则称![]() 为带宽.
为带宽.
(1)判断函数![]() 是不是带状函数?如果是,指出带宽(不用证明);如果不是,说明理由;
是不是带状函数?如果是,指出带宽(不用证明);如果不是,说明理由;
(2)求证:函数![]() (
(![]() )是带状函数;
)是带状函数;
(3)求证:函数![]() (
(![]() )为带状函数的充要条件是
)为带状函数的充要条件是![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图是函数![]() 一个周期内的图象,将
一个周期内的图象,将![]() 图象上所有点的横坐标伸长为原来的2倍,纵坐标不变,再把所得图象向右平移
图象上所有点的横坐标伸长为原来的2倍,纵坐标不变,再把所得图象向右平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象.
的图象.
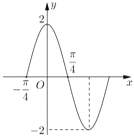
(1)求函数![]() 和
和![]() 的解析式;
的解析式;
(2)若![]() ,求
,求![]() 的所有可能的值;
的所有可能的值;
(3)求函数![]() (
(![]() 为正常数)在区间
为正常数)在区间![]() 内的所有零点之和.
内的所有零点之和.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com