
科目: 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面是边长为2的正方形,
中,底面是边长为2的正方形,![]() ,
,![]() 为
为![]() 中点,点
中点,点![]() 在
在![]() 上且
上且![]() 平面
平面![]() ,
,![]() 在
在![]() 延长线上,
延长线上,![]() ,交
,交![]() 于
于![]() ,且
,且![]()

(1)证明:![]() 平面
平面![]() ;
;
(2)设点![]() 在线段
在线段![]() 上,若二面角
上,若二面角![]() 为
为![]() ,求
,求![]() 的长度.
的长度.
查看答案和解析>>
科目: 来源: 题型:
【题目】我国是全球最大的口罩生产国,在2020年3月份,我国每日口罩产量超一亿只,已基本满足国内人民的需求,但随着疫情在全球范围扩散,境外口罩需求量激增,世界卫生组织公开呼吁扩大口罩产能常见的口罩有![]() 和
和![]() (分别阻挡不少于90.0%和95.0%的0.055到0.095微米的氯化钠颗粒)两种,某口罩厂两条独立的生产线分别生产
(分别阻挡不少于90.0%和95.0%的0.055到0.095微米的氯化钠颗粒)两种,某口罩厂两条独立的生产线分别生产![]() 和
和![]() 两种口罩,为保证质量对其进行多项检测并评分(满分100分),规定总分大于或等于85分为合格,小于85分为次品,现从流水线上随机抽取这两种口罩各100个进行检测并评分,结果如下:
两种口罩,为保证质量对其进行多项检测并评分(满分100分),规定总分大于或等于85分为合格,小于85分为次品,现从流水线上随机抽取这两种口罩各100个进行检测并评分,结果如下:
总分 |
|
|
|
|
|
| 6 | 14 | 42 | 31 | 7 |
| 4 | 6 | 47 | 35 | 8 |
(1)试分别估计两种口罩的合格率;
(2)假设生产一个![]() 口罩,若质量合格,则盈利3元,若为次品则亏损1元;生产一个
口罩,若质量合格,则盈利3元,若为次品则亏损1元;生产一个![]() 口罩,若质量合格,则盈利8元,若为次品则亏损2元,在(1)的前提下,
口罩,若质量合格,则盈利8元,若为次品则亏损2元,在(1)的前提下,
①设![]() 为生产一个
为生产一个![]() 口罩和生产一个
口罩和生产一个![]() 口罩所得利润的和,求随机变量
口罩所得利润的和,求随机变量![]() 的分布列和数学期望;
的分布列和数学期望;
②求生产4个![]() 口罩所得的利润不少于8元的概率
口罩所得的利润不少于8元的概率
查看答案和解析>>
科目: 来源: 题型:
【题目】孙子定理是中国古代求解一次同余式组的方法,是数论中一个重要定理,最早可见于中国南北朝时期的数学著作《孙子算经》,![]() 年英国来华传教士伟烈亚力将其问题的解法传至欧洲,
年英国来华传教士伟烈亚力将其问题的解法传至欧洲,![]() 年英国数学家马西森指出此法符合
年英国数学家马西森指出此法符合![]() 年由高斯得出的关于同余式解法的一般性定理,因而西方称之为“中国剩余定理”.这个定理讲的是一个关于整除的问题,现有这样一个整除问题:将
年由高斯得出的关于同余式解法的一般性定理,因而西方称之为“中国剩余定理”.这个定理讲的是一个关于整除的问题,现有这样一个整除问题:将![]() 至
至![]() 这
这![]() 个整数中能被
个整数中能被![]() 除余
除余![]() 且被
且被![]() 除余
除余![]() 的数按由小到大的顺序排成一列构成一数列,则此数列的项数是( )
的数按由小到大的顺序排成一列构成一数列,则此数列的项数是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
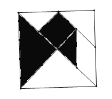
【题目】七巧板是中国古代劳动人民的发明,其历史至少可以追溯到公元前一世纪,后清陆以湉《冷庐杂识》卷一中写道“近又有七巧图,其式五,其数七,其变化之式多至千余”在18世纪,七巧板流传到了国外,被誉为“东方魔板”,至今英国剑桥大学的图书馆里还珍藏着一部《七巧新谱》.完整图案为一正方形(如图):五块等腰直角三角形、一块正方形和一块平行四边形,如果在此正方形中随机取一点,那么此点取自阴影部分的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,满足
,满足![]() .
.
(1)求证:数列![]() 等差数列;
等差数列;
(2)当![]() 时,记
时,记![]() ,是否存在正整数
,是否存在正整数![]() 、
、![]() ,使得
,使得![]() 、
、![]() 、
、![]() 成等比数列?若存在,求出所有满足条件的数对
成等比数列?若存在,求出所有满足条件的数对![]() ;若不存在,请说明理由;
;若不存在,请说明理由;
(3)若数列![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 是公比为
是公比为![]() 的等比数列,求最小正整数
的等比数列,求最小正整数![]() ,使得当
,使得当![]() 时,
时,![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() .
.
(1)求函数![]() 的图象在
的图象在![]() (
(![]() 为自然对数的底数)处的切线方程;
为自然对数的底数)处的切线方程;
(2)若对任意的![]() ,均有
,均有![]() ,则称
,则称![]() 为
为![]() 在区间
在区间![]() 上的下界函数,
上的下界函数,![]() 为
为![]() 在区间
在区间![]() 上的上界函数.
上的上界函数.
①若![]() ,求证:
,求证:![]() 为
为![]() 在
在![]() 上的上界函数;
上的上界函数;
②若![]() ,
,![]() 为
为![]() 在
在![]() 上的下界函数,求实数
上的下界函数,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图![]() ,某十字路口的花圃中央有一个底面半径为
,某十字路口的花圃中央有一个底面半径为![]() 的圆柱形花柱,四周斑马线的内侧连线构成边长为
的圆柱形花柱,四周斑马线的内侧连线构成边长为![]() 的正方形.因工程需要,测量员将使用仪器沿斑马线的内侧进行测量,其中仪器
的正方形.因工程需要,测量员将使用仪器沿斑马线的内侧进行测量,其中仪器![]() 的移动速度为
的移动速度为![]() ,仪器
,仪器![]() 的移动速度为
的移动速度为![]() .若仪器
.若仪器![]() 与仪器
与仪器![]() 的对视光线被花柱阻挡,则称仪器
的对视光线被花柱阻挡,则称仪器![]() 在仪器
在仪器![]() 的“盲区”中.
的“盲区”中.



(1)如图![]() ,斑马线的内侧连线构成正方形
,斑马线的内侧连线构成正方形![]() ,仪器
,仪器![]() 在点
在点![]() 处,仪器
处,仪器![]() 在
在![]() 上距离点
上距离点![]()
![]() 处,试判断仪器
处,试判断仪器![]() 是否在仪器
是否在仪器![]() 的“盲区”中,并说明理由;
的“盲区”中,并说明理由;
(2)如图![]() ,斑马线的内侧连线构成正方形
,斑马线的内侧连线构成正方形![]() ,仪器
,仪器![]() 从点
从点![]() 出发向点
出发向点![]() 移动,同时仪器
移动,同时仪器![]() 从点
从点![]() 出发向点
出发向点![]() 移动,在这个移动过程中,仪器
移动,在这个移动过程中,仪器![]() 在仪器
在仪器![]() 的“盲区”中的时长为多少?
的“盲区”中的时长为多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() 的左顶点为
的左顶点为![]() ,右焦点为
,右焦点为![]() ,过原点
,过原点![]() 的直线(与坐标轴不重合)与椭圆
的直线(与坐标轴不重合)与椭圆![]() 交于点
交于点![]() 、
、![]() ,直线
,直线![]() 、
、![]() 分别与
分别与![]() 轴交于点
轴交于点![]() 、
、![]() .
.
(1)若![]() ,求点
,求点![]() 的横坐标;
的横坐标;
(2)设直线![]() 、
、![]() 的斜率分别为
的斜率分别为![]() 、
、![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com