
科目: 来源: 题型:
【题目】已知椭圆![]()
![]() 的离心率为
的离心率为![]() ,焦距为
,焦距为![]() ,直线
,直线![]() 过椭圆的
过椭圆的![]() 左焦点.
左焦点.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若直线![]() 与
与![]() 轴交于点
轴交于点![]() 是椭圆
是椭圆![]() 上的两个动点,
上的两个动点,![]() 的平分线在
的平分线在![]() 轴上,
轴上,![]() .试判断直线
.试判断直线![]() 是否过定点,若过定点,求出定点坐标;若不过定点,请说明理由.
是否过定点,若过定点,求出定点坐标;若不过定点,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】2019年春节期间,我国高速公路继续执行“节假日高速公路免费政策”某路桥公司为掌握春节期间车辆出行的高峰情况,在某高速公路收费点记录了大年初三上午9:20~10:40这一时间段内通过的车辆数,统计发现这一时间段内共有600辆车通过该收费点,它们通过该收费点的时刻的频率分布直方图如下图所示,其中时间段9:20~9:40记作区间![]() ,9:40~10:00记作
,9:40~10:00记作![]() ,10:00~10:20记作
,10:00~10:20记作![]() ,10:20~10:40记作
,10:20~10:40记作![]() .例如:10点04分,记作时刻64.
.例如:10点04分,记作时刻64.

(1)估计这600辆车在9:20~10:40时间段内通过该收费点的时刻的平均值(同一组中的数据用该组区间的中点值代表);
(2)为了对数据进行分析,现采用分层抽样的方法从这600辆车中抽取10辆,再从这10辆车中随机抽取4辆,设抽到的4辆车中,在9:20~10:00之间通过的车辆数为X,求X的分布列与数学期望;
(3)由大数据分析可知,车辆在每天通过该收费点的时刻T服从正态分布![]() ,其中
,其中![]() 可用这600辆车在9:20~10:40之间通过该收费点的时刻的平均值近似代替,
可用这600辆车在9:20~10:40之间通过该收费点的时刻的平均值近似代替,![]() 可用样本的方差近似代替(同一组中的数据用该组区间的中点值代表),已知大年初五全天共有1000辆车通过该收费点,估计在9:46~10:40之间通过的车辆数(结果保留到整数).
可用样本的方差近似代替(同一组中的数据用该组区间的中点值代表),已知大年初五全天共有1000辆车通过该收费点,估计在9:46~10:40之间通过的车辆数(结果保留到整数).
参考数据:若![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,四棱锥S﹣ABCD中,SD=CD=SC=2AB=2BC,平面ABCD⊥底面SDC,AB∥CD,∠ABC=90°,E是SD中点.
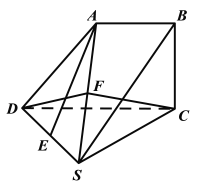
(1)证明:直线AE//平面SBC;
(2)点F为线段AS的中点,求二面角F﹣CD﹣S的大小.
查看答案和解析>>
科目: 来源: 题型:
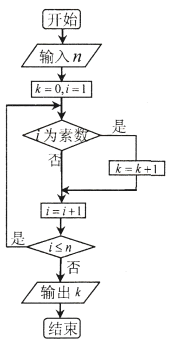
【题目】2018年9月24日,阿贝尔奖和菲尔兹奖双料得主、英国著名数学家阿蒂亚爵士宣布自己证明了黎曼猜想,这一事件引起了数学界的震动,在1859年,德国数学家黎曼向科学院提交了题目为《论小于某值的素数个数》的论文并提出了一个命题,也就是著名的黎曼猜想.在此之前,著名数学家欧拉也曾研究过这个问题,并得到小于数字![]() 的素数个数大约可以表示为
的素数个数大约可以表示为![]() 的结论(素数即质数,
的结论(素数即质数,![]() ).根据欧拉得出的结论,如下流程图中若输入
).根据欧拉得出的结论,如下流程图中若输入![]() 的值为
的值为![]() ,则输出
,则输出![]() 的值应属于区间( )
的值应属于区间( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】某运动制衣品牌为了成衣尺寸更精准,现选择15名志愿者,对其身高和臂展进行测量(单位:厘米),左图为选取的15名志愿者身高与臂展的折线图,右图为身高与臂展所对应的散点图,并求得其回归方程为![]() ,以下结论中不正确的为
,以下结论中不正确的为


A. 15名志愿者身高的极差小于臂展的极差
B. 15名志愿者身高和臂展成正相关关系,
C. 可估计身高为190厘米的人臂展大约为189.65厘米,
D. 身高相差10厘米的两人臂展都相差11.6厘米,
查看答案和解析>>
科目: 来源: 题型:
【题目】已知长方形ABCD中,AB=1,∠ABD=60°,现将长方形ABCD沿着对角线BD折起,使平面ABD⊥平面BCD,则折后几何图形的外接球表面积为_____.
查看答案和解析>>
科目: 来源: 题型:
【题目】以直角坐标系的原点为极点,![]() 轴的非负半轴为极轴建立极坐标系,曲线
轴的非负半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数).
为参数).
(1)求曲线![]() 的参数方程与直线
的参数方程与直线![]() 的普通方程;
的普通方程;
(2)设点过![]() 为曲线
为曲线![]() 上的动点,点
上的动点,点![]() 和点
和点![]() 为直线
为直线![]() 上的点,且满足
上的点,且满足![]() 为等边三角形,求
为等边三角形,求![]() 边长的取值范围.
边长的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)=axex,g(x)=x2+2x+b,若曲线y=f(x)与曲线y=g(x)都过点P(1,c).且在点P处有相同的切线l.
(Ⅰ)求切线l的方程;
(Ⅱ)若关于x的不等式k[ef(x)]≥g(x)对任意x∈[﹣1,+∞)恒成立,求实数k的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知O为坐标原点,抛物线E的方程为x2=2py(p>0),其焦点为F,过点M (0,4)的直线![]() 与抛物线相交于P、Q两点且△OPQ为以O为直角顶点的直角三角形.
与抛物线相交于P、Q两点且△OPQ为以O为直角顶点的直角三角形.
(Ⅰ)求E的方程;
(Ⅱ)设点N为曲线E上的任意一点,证明:以FN为直径的圆与x轴相切.
查看答案和解析>>
科目: 来源: 题型:
【题目】四棱锥P﹣ABCD中,AB∥CD,AB⊥BC,AB=BC=1,PA=CD=2,PA⊥平面ABCD,E在棱PB上.
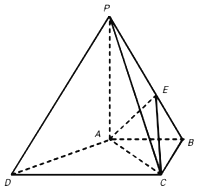
(Ⅰ)求证:AC⊥PD;
(Ⅱ)若VP﹣ACE![]() ,求证:PD∥平面AEC.
,求证:PD∥平面AEC.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com