
����Ŀ��2018��9��24�գ����������ͷƶ��Ƚ�˫�ϵ�����Ӣ��������ѧ�Ұ����Ǿ�ʿ�����Լ�֤�����������룬��һ�¼���������ѧ�������1859�꣬�¹���ѧ���������ѧԺ�ύ����ĿΪ����С��ijֵ�����������������IJ������һ�����⣬Ҳ������������������.�ڴ�֮ǰ��������ѧ��ŷ��Ҳ���о���������⣬���õ�С������![]() ������������Լ���Ա�ʾΪ
������������Լ���Ա�ʾΪ![]() �Ľ��ۣ�������������
�Ľ��ۣ�������������![]() ��.����ŷ���ó��Ľ��ۣ���������ͼ��������
��.����ŷ���ó��Ľ��ۣ���������ͼ��������![]() ��ֵΪ
��ֵΪ![]() �������
�������![]() ��ֵӦ�������䣨 ��
��ֵӦ�������䣨 ��
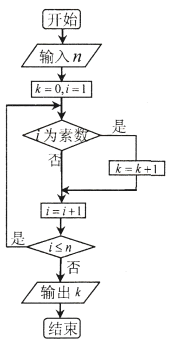
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
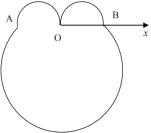
����Ŀ����ͼ���ڼ�����ϵ![]() �У�
��![]() ��
��![]() ����
����![]() ��
��![]() ��
��![]() ����Բ��Բ�ķֱ�Ϊ
����Բ��Բ�ķֱ�Ϊ![]() ��
��![]() ��
��![]() ������
������![]() �ǻ�
�ǻ�![]() ������
������![]() �ǻ�
�ǻ�![]() ������
������![]() �ǻ�
�ǻ�![]() ��
��
��1�������![]() ��
��![]() ��
��![]() �ļ����귽�̣�
�ļ����귽�̣�
��2������![]() ��
��![]() ��
��![]() ��
��![]() ���ɣ�������
���ɣ�������![]() �ļ����귽��Ϊ
�ļ����귽��Ϊ![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ���������
���������![]() ������
������![]() �����й����㣨�������⣩�ļ����꣮
�����й����㣨�������⣩�ļ����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����P��ABCD�У�����PAD�͵���ABCD����BAD��60�㣬��PAD�DZ߳�Ϊ2���������Σ�����ABCD�����Σ���MΪPC���е�.
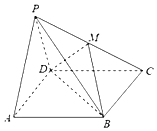
��1����֤��PA��ƽ��MDB��
��2��������A��BDM�����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ԲC��![]() ��
��![]() ������
������![]() ��
��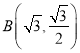 ��
��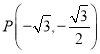 ��
��![]() �ĵ������ҽ�������������C�ϣ�
�ĵ������ҽ�������������C�ϣ�
��1������ԲC�ı����̣�
��2����OΪ����ԭ�㣬FΪ��ԲC���ҽ��㣬����F��ֱ��l�ֱ�����ԲC����M��N���㣬![]() ����֤��ֱ��
����֤��ֱ��![]() ��
��![]() ����x��Գƣ�
����x��Գƣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪OΪ����ԭ�㣬������E�ķ���Ϊx2��2py��p��0�����佹��ΪF������M ��0��4����ֱ��![]() ���������ཻ��P��Q��������OPQΪ��OΪֱ�Ƕ����ֱ�������Σ�
���������ཻ��P��Q��������OPQΪ��OΪֱ�Ƕ����ֱ�������Σ�
������E�ķ��̣�
�������NΪ����E�ϵ�����һ�㣬֤������FNΪֱ����Բ��x�����У�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У�������ԭ��OΪ���㣬��x��������Ϊ���ᣬ����������ϵ������C�ļ����귽��Ϊ![]() ����
����![]() ������C�ڵ�A,��б��Ϊ����ֱ��l���߶�OA���е�B��������C����P��Q����.
������C�ڵ�A,��б��Ϊ����ֱ��l���߶�OA���е�B��������C����P��Q����.
(1)������C��ֱ�����귽�̼�ֱ��l�IJ�������;
(2)��ֱ��l��б����Ϊ��ֵʱ, |BP|��|BQ|ȡ��Сֵ, �����|BP|��|BQ|��Сֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪˫����![]() �����ҽ���ֱ�ΪF1��F2������F1��Բx2+y2��a2�����߽�˫������֧�ڵ�M����tan��F1MF2��2����eΪ˫���ߵ������ʣ���e2��ֵΪ�� ��
�����ҽ���ֱ�ΪF1��F2������F1��Բx2+y2��a2�����߽�˫������֧�ڵ�M����tan��F1MF2��2����eΪ˫���ߵ������ʣ���e2��ֵΪ�� ��
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Բ![]() ��һ������Ϊ
��һ������Ϊ![]() ������
������![]() ������һ�㵽
������һ�㵽![]() �ľ�����ڸõ㵽ֱ��
�ľ�����ڸõ㵽ֱ��![]() �ľ��룮
�ľ��룮
������![]() ������
������![]() �ķ��̣�
�ķ��̣�
������ֱ��![]() ����Բֻ��һ������
����Բֻ��һ������![]() ��������
��������![]() ����
����![]() ���㣬��
���㣬��![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() �У�����
������![]() ����
����![]() ������������
������������![]() ���������Σ�E��BC�е㣬������������ȷ���ǣ� ��
���������Σ�E��BC�е㣬������������ȷ���ǣ� ��

A.![]() ��
��![]() ������ֱ��B.
������ֱ��B.![]() ƽ��
ƽ��![]()
C.AE��![]() Ϊ����ֱ�ߣ���
Ϊ����ֱ�ߣ���![]() D.
D.![]() ƽ��
ƽ��![]()
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com