
科目: 来源: 题型:
【题目】已知点F是拋物线C:y2=2px(p>0)的焦点,点M(x0,1)在C上,且|MF|=![]() .
.
(1)求p的值;
(2)若直线l经过点Q(3,-1)且与C交于A,B(异于M)两点,证明:直线AM与直线BM的斜率之积为常数.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,四边形ABCD为等腰梯形,AB=4,AD=DC=CB=2,△ADC沿AC折起,使得平面ADC⊥平面ABC,E为AB的中点,连接DE,DB(如图2).
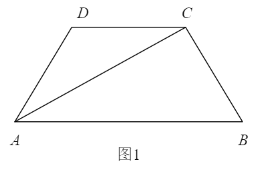
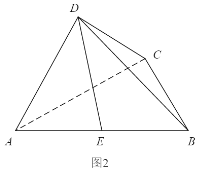
(1)求证:BC⊥AD
(2)求直线DE与平面BCD所成的角的正弦值.
查看答案和解析>>
科目: 来源: 题型:
【题目】我国是世界严重缺水的国家,城市缺水问题较为突出,某市政府为了鼓励居民节约用水,计划在本市试行居民生活用水定额管理,即确定一个合理的居民月用水量标准![]() (吨),用水量不超过
(吨),用水量不超过![]() 的部分按平价收费,超过
的部分按平价收费,超过![]() 的部分按议价收费,为了了解全市民月用水量的分布情况,通过抽样,获得了100位居民某年的月用水量(单位:吨),将数据按照
的部分按议价收费,为了了解全市民月用水量的分布情况,通过抽样,获得了100位居民某年的月用水量(单位:吨),将数据按照![]() 分成9组,制成了如图所示的频率分布直方图.
分成9组,制成了如图所示的频率分布直方图.

(Ⅰ)若全市居民中月均用水量不低于3吨的人数为3.6万,试估计全市有多少居民?并说明理由;
(Ⅱ)若该市政府拟采取分层抽样的方法在用水量吨数为![]() 和
和![]() 之间选取7户居民作为议价水费价格听证会的代表,并决定会后从这7户家庭中按抽签方式选出4户颁发“低碳环保家庭”奖,设
之间选取7户居民作为议价水费价格听证会的代表,并决定会后从这7户家庭中按抽签方式选出4户颁发“低碳环保家庭”奖,设![]() 为用水量吨数在
为用水量吨数在![]() 中的获奖的家庭数,
中的获奖的家庭数,![]() 为用水量吨数在
为用水量吨数在![]() 中的获奖家庭数,记随机变量
中的获奖家庭数,记随机变量![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)![]() |2x﹣3|,g(x)
|2x﹣3|,g(x)![]() |2x+a+b|.
|2x+a+b|.
(1)解不等式f(x)![]() x2;
x2;
(2)当a![]() 0,b
0,b![]() 0时,若F(x)
0时,若F(x)![]() f(x)+g(x)的值域为[5,+∞),求证:
f(x)+g(x)的值域为[5,+∞),求证:![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系xOy中,将曲线方程![]() ,先向左平移2个单位,再向上平移2个单位,得到曲线C.
,先向左平移2个单位,再向上平移2个单位,得到曲线C.
(1)点M(x,y)为曲线C上任意一点,写出曲线C的参数方程,并求出![]() 的最大值;
的最大值;
(2)设直线l的参数方程为![]() ,(t为参数),又直线l与曲线C的交点为E,F,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,求过线段EF的中点且与l垂直的直线的极坐标方程.
,(t为参数),又直线l与曲线C的交点为E,F,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,求过线段EF的中点且与l垂直的直线的极坐标方程.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,定义:以椭圆中心为圆心,长轴为直径的圆叫做椭圆的“辅助圆”.过椭圆第四象限内一点M作x轴的垂线交其“辅助圆”于点N,当点N在点M的下方时,称点N为点M的“下辅助点”.已知椭圆E:![]() 上的点
上的点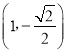 的下辅助点为(1,﹣1).
的下辅助点为(1,﹣1).
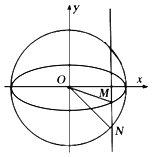
(1)求椭圆E的方程;
(2)若△OMN的面积等于![]() ,求下辅助点N的坐标;
,求下辅助点N的坐标;
(3)已知直线l:x﹣my﹣t=0与椭圆E交于不同的A,B两点,若椭圆E上存在点P,满足![]() ,求直线l与坐标轴围成的三角形面积的最小值.
,求直线l与坐标轴围成的三角形面积的最小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)=ax﹣sinx(a∈R).
(1)当![]() 时,f(x)
时,f(x)![]() 0恒成立,求正实数a的取值范围;
0恒成立,求正实数a的取值范围;
(2)当a≥1时,探索函数F(x)![]() f(x)﹣cosx+a﹣1在(0,π)上的零点个数,并说明理由.
f(x)﹣cosx+a﹣1在(0,π)上的零点个数,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在长方体ABCD﹣HKLE中,底面ABCD是边长为3的正方形,对角线AC与BD相交于点O,点F在线段AH上且![]() ,BE与底面ABCD所成角为
,BE与底面ABCD所成角为![]() .
.
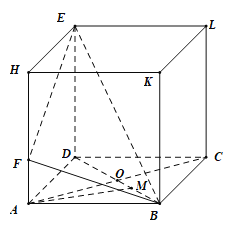
(1)求证:AC⊥BE;
(2)M为线段BD上一点,且![]() ,求异面直线AM与BF所成角的余弦值.
,求异面直线AM与BF所成角的余弦值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某中学举行的“新冠肺炎”防控知识闭卷考试比赛,总分获得一等奖、二等奖、三等奖的代表队人数情况如下表,该校政教处为使颁奖仪式有序进行,气氛活跃,在颁奖过程中穿插抽奖活动,并用分层抽样的方法从三个代表队中共抽取16人在前排就坐,其中一等奖代表队有6人.
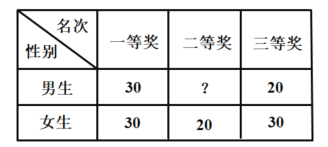
(1)求二等奖代表队的男生人数;
(2)从前排就坐的三等奖代表队员5人(2男3女)中随机抽取3人上台领奖,请求出只有一个男生上台领奖的概率;
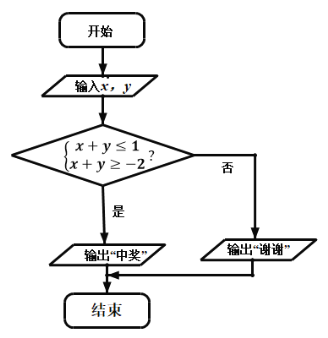
(3)抽奖活动中,代表队员通过操作按键,使电脑自动产生[![]() 2,2]内的两个均匀随机数x,y,随后电脑自动运行如图所示的程序框图的相应程序,若电脑显示“中奖”,则代表队员获相应奖品;若电脑显示“谢谢”,则不中奖,求代表队队员获得奖品的概率.
2,2]内的两个均匀随机数x,y,随后电脑自动运行如图所示的程序框图的相应程序,若电脑显示“中奖”,则代表队员获相应奖品;若电脑显示“谢谢”,则不中奖,求代表队队员获得奖品的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的部分图象如图所示,又函数![]() .
.
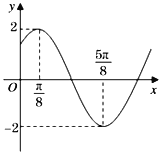
(1)求函数![]() 的单调减区间;
的单调减区间;
(2)设△ABC的内角A,B,C的对边分别为a,b,c,又![]() ,且锐角C满足
,且锐角C满足![]() ,若sinB=2sinA,求a+b的值.
,若sinB=2sinA,求a+b的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com