
科目: 来源: 题型:
【题目】设{an}是一个首项为2,公比为q(q![]() 1)的等比数列,且3a1,2a2,a3成等差数列.
1)的等比数列,且3a1,2a2,a3成等差数列.
(1)求{an}的通项公式;
(2)已知数列{bn}的前n项和为Sn,b1=1,且![]() 1(n≥2),求数列{an
1(n≥2),求数列{an![]() bn}的前n项和Tn.
bn}的前n项和Tn.
查看答案和解析>>
科目: 来源: 题型:
【题目】在矩形ABCD中,![]() ,
,![]() ,沿矩形对角线BD将
,沿矩形对角线BD将![]() 折起形成四面体ABCD,在这个过程中,现在下面四个结论:①在四面体ABCD中,当
折起形成四面体ABCD,在这个过程中,现在下面四个结论:①在四面体ABCD中,当![]() 时,
时,![]() ;②四面体ABCD的体积的最大值为
;②四面体ABCD的体积的最大值为![]() ;③在四面体ABCD中,BC与平面ABD所成角可能为
;③在四面体ABCD中,BC与平面ABD所成角可能为![]() ;④四面体ABCD的外接球的体积为定值.其中所有正确结论的编号为( )
;④四面体ABCD的外接球的体积为定值.其中所有正确结论的编号为( )
A.①④B.①②C.①②④D.②③④
查看答案和解析>>
科目: 来源: 题型:
【题目】著名数学家华罗庚先生曾说过:“数缺形时少直观,形缺数时难入微数形结合百般好,隔裂分家万事休.”在数学的学习和研究中,我们经常用函数的图象来研究函数的性质,也经常用函数的解析式来琢磨函数的图象的特征,如某体育品牌的LOGO为![]() ,可抽象为如图所示的轴对称的优美曲线,下列函数中,其图象大致可“完美”局部表达这条曲线的函数是( )
,可抽象为如图所示的轴对称的优美曲线,下列函数中,其图象大致可“完美”局部表达这条曲线的函数是( )
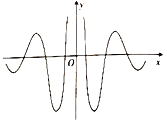
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】某公司对旗下的甲、乙两个门店在1至9月份的营业额(单位:万元)进行统计并得到如图折线图.
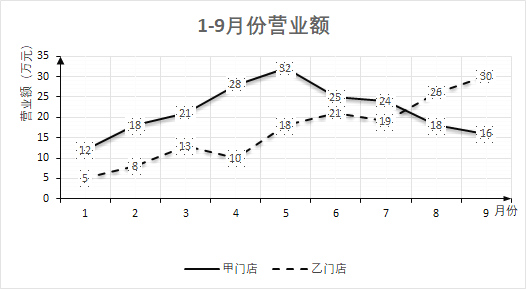
下面关于两个门店营业额的分析中,错误的是( )
A.甲门店的营业额折线图具有较好的对称性,故而营业额的平均值约为32万元
B.根据甲门店的营业额折线图可知,该门店营业额的平均值在[20,25]内
C.根据乙门店的营业额折线图可知,其营业额总体是上升趋势
D.乙门店在这9个月份中的营业额的极差为25万元
查看答案和解析>>
科目: 来源: 题型:
【题目】双曲线C的渐近线方程为![]() ,一个焦点为F(0,﹣8),则该双曲线的标准方程为_____.已知点A(﹣6,0),若点P为C上一动点,且P点在x轴上方,当点P的位置变化时,△PAF的周长的最小值为_____.
,一个焦点为F(0,﹣8),则该双曲线的标准方程为_____.已知点A(﹣6,0),若点P为C上一动点,且P点在x轴上方,当点P的位置变化时,△PAF的周长的最小值为_____.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知抛物线![]() 上的点
上的点![]() 到焦点的距离为
到焦点的距离为![]() .
.

(1)求![]() 的值;
的值;
(2)如上图,已知动线段![]() (
(![]() 在
在![]() 的右边)在直线
的右边)在直线![]() 上,且
上,且![]() ,现过
,现过![]() 作
作![]() 的切线,取左边的切点
的切线,取左边的切点![]() ,过
,过![]() 作
作![]() 的切线,取右边的切点为
的切线,取右边的切点为![]() ,当
,当![]() ,求
,求![]() 点的横坐标
点的横坐标![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知数列{an}满足,an+2=3an+1﹣2an,a1=1,a2=3,记bn![]() ,Sn为数列{bn}的前n项和.
,Sn为数列{bn}的前n项和.
(1)求证:{an+1﹣an}为等比数列,并求an;
(2)求证:Sn![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,△PAD为等边三角形,AB=AD![]() CD=2,∠BAD=∠ADC=90°,∠PDC=60°,E为BC的中点.
CD=2,∠BAD=∠ADC=90°,∠PDC=60°,E为BC的中点.
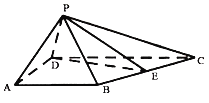
(1)证明:AD⊥PE.
(2)求直线PA与平面PDE所成角的大小.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知数列{an}满足,an+1=an+1![]() ,a1=a,则一定存在a,使数列中( )
,a1=a,则一定存在a,使数列中( )
A.存在n∈N*,有an+1an+2<0
B.存在n∈N*,有(an+1﹣1)(an+2﹣1)<0
C.存在n∈N*,有![]()
D.存在n∈N*,有![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com