
科目: 来源: 题型:
【题目】为了治理空气污染,某市设![]() 个监测站用于监测空气质量指数
个监测站用于监测空气质量指数![]() ,其中在轻度污染区、中度污染区、重度污染区分别设有
,其中在轻度污染区、中度污染区、重度污染区分别设有![]() 、
、![]() 、
、![]() 个监测站,并以
个监测站,并以![]() 个监测站测得的
个监测站测得的![]() 的平均值为依据播报该市的空气质量.
的平均值为依据播报该市的空气质量.
(1)若某日播报的![]() 为
为![]() ,已知轻度污染区
,已知轻度污染区![]() 平均值为
平均值为![]() ,中度污染区
,中度污染区![]() 平均值为
平均值为![]() ,求重试污染区
,求重试污染区![]() 平均值;
平均值;
(2)如图是![]() 年
年![]() 月份
月份![]() 天的
天的![]() 的频率分布直方图,
的频率分布直方图,![]() 月份仅有
月份仅有![]() 天
天![]() 在
在![]() 内.
内.
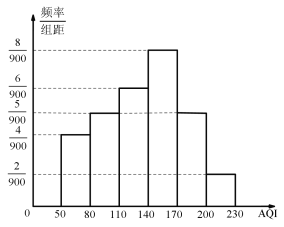
①某校参照官方公布的![]() ,如果周日
,如果周日![]() 小于
小于![]() 就组织学生参加户外活动,以统计数据中的频率为概率,求该校学生周日能参加户外活动的概率;
就组织学生参加户外活动,以统计数据中的频率为概率,求该校学生周日能参加户外活动的概率;
②环卫部门从![]() 月份
月份![]() 不小于
不小于![]() 的数据中抽取两天的数据进行研究,求抽取的这两天中
的数据中抽取两天的数据进行研究,求抽取的这两天中![]() 值都在
值都在![]() 的概率.
的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】设![]() ,
,![]() 分别是椭圆
分别是椭圆![]() 的左,右焦点,
的左,右焦点,![]() 两点分别是椭圆
两点分别是椭圆![]() 的上,下顶点,
的上,下顶点,![]() 是等腰直角三角形,延长
是等腰直角三角形,延长![]() 交椭圆
交椭圆![]() 于
于![]() 点,且
点,且![]() 的周长为
的周长为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设点![]() 是椭圆
是椭圆![]() 上异于
上异于![]() 的动点,直线
的动点,直线![]() 与直
与直![]() 分别相交于
分别相交于![]() 两点,点
两点,点![]() ,求证:
,求证:![]() 的外接圆恒过原点
的外接圆恒过原点![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】按照水果市场的需要等因素,水果种植户把某种成熟后的水果按其直径![]() 的大小分为不同等级.某商家计划从该种植户那里购进一批这种水果销售.为了了解这种水果的质量等级情况,现随机抽取了100个这种水果,统计得到如下直径分布表(单位:mm):
的大小分为不同等级.某商家计划从该种植户那里购进一批这种水果销售.为了了解这种水果的质量等级情况,现随机抽取了100个这种水果,统计得到如下直径分布表(单位:mm):
d |
|
|
|
|
|
等级 | 三级品 | 二级品 | 一级品 | 特级品 | 特级品 |
频数 | 1 | m | 29 | n | 7 |
用分层抽样的方法从其中的一级品和特级品共抽取6个,其中一级品2个.
(1)估计这批水果中特级品的比例;
(2)已知样本中这批水果不按等级混装的话20个约1斤,该种植户有20000斤这种水果待售,商家提出两种收购方案:
方案A:以6.5元/斤收购;
方案B:以级别分装收购,每袋20个,特级品8元/袋,一级品5元/袋,二级品4元/袋,三级品3元/袋.
用样本的频率分布估计总体分布,问哪个方案种植户的收益更高?并说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知![]() 为等差数列,各项为正的等比数列
为等差数列,各项为正的等比数列![]() 的前n项和为
的前n项和为![]() , ,且
, ,且![]() ,
,![]() ,.在①
,.在①![]() ;②
;②![]() ;③
;③![]() 这三个条件中任选其中一个,补充在上面的横线上,并完成下面问题的解答(如果选择多个条件解答,则按选择第一个解答计分).
这三个条件中任选其中一个,补充在上面的横线上,并完成下面问题的解答(如果选择多个条件解答,则按选择第一个解答计分).
(1)求数列![]() 和
和![]() 的通项公式;
的通项公式;
(2)求数列![]() 的前
的前![]() 项和
项和![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】某保险公司为客户定制了5个险种:甲,一年期短险;乙,两全保险;丙,理财类保险;丁,定期寿险:戊,重大疾病保险,各种保险按相关约定进行参保与理赔.该保险公司对5个险种参保客户进行抽样调查,得出如下的统计图例,以下四个选项错误的是( )



A.54周岁以上参保人数最少B.18~29周岁人群参保总费用最少
C.丁险种更受参保人青睐D.30周岁以上的人群约占参保人群的80%
查看答案和解析>>
科目: 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的普通方程为
的普通方程为![]() ,直线
,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),其中
为参数),其中![]() .以坐标
.以坐标![]() 为极点,以
为极点,以![]() 轴非负半轴为极轴,建立极坐标系.
轴非负半轴为极轴,建立极坐标系.
(1)求曲线![]() 的极坐标方程和直线
的极坐标方程和直线![]() 的普通方程;
的普通方程;
(2)设点![]() ,
,![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 与
与![]() 的交点分别为
的交点分别为![]() ,
,![]() .当
.当![]() 为等腰直角三角形时,求直线
为等腰直角三角形时,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目: 来源: 题型:
【题目】动点![]() 与定点
与定点![]() 的距离和该动点到直线
的距离和该动点到直线![]() 的距离的比是常数
的距离的比是常数![]() .
.
(1)求动点![]() 轨迹方程
轨迹方程![]() ;
;
(2)已知点![]() ,问在
,问在![]() 轴上是否存在一点
轴上是否存在一点![]() ,使得过
,使得过![]() 点的任一条斜率不为0的弦交曲线
点的任一条斜率不为0的弦交曲线![]() 于
于![]() 两点,都有
两点,都有![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】现从某学校中选出![]() 名学生,统计了
名学生,统计了![]() 名学生一周的户外运动时间(分钟)总和,得到如图所示的频率分布直方图和统计表格.
名学生一周的户外运动时间(分钟)总和,得到如图所示的频率分布直方图和统计表格.

(1)写出![]() 的值,并估计该学校人均每周的户外运动时间(同一组数据用该组区间的中点值作代表);
的值,并估计该学校人均每周的户外运动时间(同一组数据用该组区间的中点值作代表);
(2)假设![]() ,则户外运动时长为
,则户外运动时长为![]() 的学生中,男生人数比女生人数多的概率.
的学生中,男生人数比女生人数多的概率.
(3)若![]() ,完成下列
,完成下列![]() 列联表,并回答能否有90%的把握认为“每周至少运动130分钟与性别有关”?
列联表,并回答能否有90%的把握认为“每周至少运动130分钟与性别有关”?
每周户外运动时间不少于130分钟 | 每周户外运动时间少于130分钟 | 合计 | |
男 | |||
女 | |||
合计 |
附: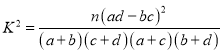 ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]()
(1)当x∈[0,π]时,f(x)≥0恒成立,求实数a的取值范围;(参考数据:sin1≈0.84)
(2)当a=1时,数列{an}满足:0<an<1,![]() =f(an),求证:{an}是递减数列.
=f(an),求证:{an}是递减数列.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com