
【题目】已知![]() 为等差数列,各项为正的等比数列
为等差数列,各项为正的等比数列![]() 的前n项和为
的前n项和为![]() , ,且
, ,且![]() ,
,![]() ,.在①
,.在①![]() ;②
;②![]() ;③
;③![]() 这三个条件中任选其中一个,补充在上面的横线上,并完成下面问题的解答(如果选择多个条件解答,则按选择第一个解答计分).
这三个条件中任选其中一个,补充在上面的横线上,并完成下面问题的解答(如果选择多个条件解答,则按选择第一个解答计分).
(1)求数列![]() 和
和![]() 的通项公式;
的通项公式;
(2)求数列![]() 的前
的前![]() 项和
项和![]()
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() .
.
【解析】
(1)分别选择条件①②③,结合等差、等比数列的通项公式,以及![]() 和
和![]() 的关系,即可求得数列
的关系,即可求得数列![]() 和
和![]() 的通项公式;
的通项公式;
(2)由(1)求得![]() ,结合等差、等比数列的前
,结合等差、等比数列的前![]() 项和公式,利用错位相减,即可求解.
项和公式,利用错位相减,即可求解.
(1)若选①:![]() ,设等差数列
,设等差数列![]() 的公差为
的公差为![]() ,
,
由![]() ,
,![]() ,可得
,可得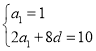 ,解得
,解得![]() ,
,
所以![]() ,
,
又由![]() ,
,
当![]() 时,由
时,由![]() ,则有
,则有![]() ,即
,即![]() ,
,
当![]() 时,
时,![]() ,整理得
,整理得![]() ,即
,即![]() ,
,
所以![]() 是以2为首项,2为公比的等比数列,
是以2为首项,2为公比的等比数列,
所以![]() .
.
(2)由(1)知![]() ,则
,则![]() ,
,
所以![]()
![]() ,
,
所以![]() .
.
(1)若选②:![]() ,设等差数列
,设等差数列![]() 的公差为d,
的公差为d,
由![]() ,
,![]() ,可得
,可得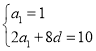 ,解得
,解得![]() ,
,
所以![]() ,所以
,所以![]() ,
,
设等比数列![]() 的公比为
的公比为![]() ,
,
因为![]() ,
,
所以![]() ,
,
又因为![]() ,所以
,所以![]() ,解得
,解得![]() 或
或![]() (舍去),
(舍去),
所以![]() .
.
(2)由(1)知![]() ,则
,则![]() ,
,
所以![]()
![]() ,
,
所以![]() .
.
(1)若选③:![]() ,设等差数列
,设等差数列![]() 的公差为
的公差为![]() ,
,
由![]() ,
,![]() ,可得
,可得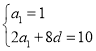 ,解得
,解得![]() ,
,
所以![]() ,
,
因为![]() ,
,![]() ,
,
当![]() ,得
,得![]() ,即
,即![]() ,解得
,解得![]() ,所以
,所以![]() .
.
(2)由(1)知![]() ,则
,则![]() ,
,
所以![]()
![]() ,
,
所以![]() .
.


 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ,直线
,直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,
两点,![]() 为坐标原点.
为坐标原点.
(1)若直线![]() 过椭圆
过椭圆![]() 的右焦点
的右焦点![]() ,求
,求![]() 的面积;
的面积;
(2)椭圆![]() 上是否存在点
上是否存在点![]() ,使得四边形
,使得四边形![]() 为平行四边形?若存在,求出所有满足条件的
为平行四边形?若存在,求出所有满足条件的![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】南宋数学家杨辉在《详解九章算法》和《算法通变本末》中,提出了一些新的垛积公式,所讨论的高阶等差数列与一般等差数列不同,前后两项之差并不相等,但是逐项差数之差或者高次差成等差数列.对这类高阶等差数列的研究,在杨辉之后一般称为“垛积术”.现有高阶等差数列,其前7项分别为1,5,11,21,37,6l,95,则该数列的第8项为( )
A.99B.131C.139D.141
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】北京2022年冬奥会和冬残奥会色彩系统的主色包括霞光红迎春黄天霁蓝长城灰瑞雪白;间色包括天青梅红竹绿冰蓝吉柿;辅助色包括墨金银.若各赛事纪念品的色彩设计要求:主色至少一种至多两种,间色两种辅助色一种,则某个纪念品的色彩搭配中包含有瑞雪白冰蓝银色这三种颜色的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现从某学校中选出![]() 名学生,统计了
名学生,统计了![]() 名学生一周的户外运动时间(分钟)总和,得到如图所示的频率分布直方图和统计表格.
名学生一周的户外运动时间(分钟)总和,得到如图所示的频率分布直方图和统计表格.

(1)写出![]() 的值,并估计该学校人均每周的户外运动时间(同一组数据用该组区间的中点值作代表);
的值,并估计该学校人均每周的户外运动时间(同一组数据用该组区间的中点值作代表);
(2)假设![]() ,则户外运动时长为
,则户外运动时长为![]() 的学生中,男生人数比女生人数多的概率.
的学生中,男生人数比女生人数多的概率.
(3)若![]() ,完成下列
,完成下列![]() 列联表,并回答能否有90%的把握认为“每周至少运动130分钟与性别有关”?
列联表,并回答能否有90%的把握认为“每周至少运动130分钟与性别有关”?
每周户外运动时间不少于130分钟 | 每周户外运动时间少于130分钟 | 合计 | |
男 | |||
女 | |||
合计 |
附: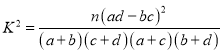 ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C :![]() 与圆
与圆![]() 相交于M,N,P,Q四点,四边形MNPQ为正方形,△PF1F2的周长为
相交于M,N,P,Q四点,四边形MNPQ为正方形,△PF1F2的周长为![]()
(1)求椭圆C的方程;
(2)设直线l与椭圆C相交于A、B两点![]() 若直线AD与直线BD的斜率之积为
若直线AD与直线BD的斜率之积为![]() ,证明:直线恒过定点.
,证明:直线恒过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国古代数学著作《孙子算经》中有这样一道算术题:“今有物不知其数,三三数之余二,五五数之余三,问物几何?”,将上述问题的所有正整数答案从小到大组成一个数列![]() ,则
,则![]() ______;
______;![]() ______.(注:三三数之余二是指此数被3除余2,例如“5”)
______.(注:三三数之余二是指此数被3除余2,例如“5”)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某省从2021年开始,高考采用取消文理分科,实行“![]() ”的模式,其中的“1”表示每位学生必须从物理、历史中选择一个科目且只能选择一个科目.某校高一年级有2000名学生(其中女生900人).该校为了解高一年级学生对“1”的选课情况,采用分层抽样的方法抽取了200名学生进行问卷调查,下表是根据调查结果得到的
”的模式,其中的“1”表示每位学生必须从物理、历史中选择一个科目且只能选择一个科目.某校高一年级有2000名学生(其中女生900人).该校为了解高一年级学生对“1”的选课情况,采用分层抽样的方法抽取了200名学生进行问卷调查,下表是根据调查结果得到的![]() 列联表.
列联表.
性别 | 选择物理 | 选择历史 | 总计 |
男生 | ________ | 50 |
|
女生 | 30 | ________ |
|
总计 | ________ | ________ | 200 |
(1)求![]() ,
,![]() 的值;
的值;
(2)请你依据该列联表判断是否有99.5%的把握认为选择科目与性别有关?说明你的理由.
| 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
附: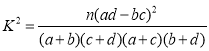 ,其中
,其中![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com