
【题目】中国古代数学著作《孙子算经》中有这样一道算术题:“今有物不知其数,三三数之余二,五五数之余三,问物几何?”,将上述问题的所有正整数答案从小到大组成一个数列![]() ,则
,则![]() ______;
______;![]() ______.(注:三三数之余二是指此数被3除余2,例如“5”)
______.(注:三三数之余二是指此数被3除余2,例如“5”)
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:高中数学 来源: 题型:
【题目】已知![]() 为等差数列,各项为正的等比数列
为等差数列,各项为正的等比数列![]() 的前n项和为
的前n项和为![]() , ,且
, ,且![]() ,
,![]() ,.在①
,.在①![]() ;②
;②![]() ;③
;③![]() 这三个条件中任选其中一个,补充在上面的横线上,并完成下面问题的解答(如果选择多个条件解答,则按选择第一个解答计分).
这三个条件中任选其中一个,补充在上面的横线上,并完成下面问题的解答(如果选择多个条件解答,则按选择第一个解答计分).
(1)求数列![]() 和
和![]() 的通项公式;
的通项公式;
(2)求数列![]() 的前
的前![]() 项和
项和![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】方舱医院的启用在本次武汉抗击新冠疫情的关键时刻起到了至关重要的作用,图1为某方舱医院的平面设计图,其结构可以看成矩形在四个角处对称地截去四个全等的三角形所得,图2中所示多边形![]() ,整体设计方案要求:内部井字形的两根水平横轴
,整体设计方案要求:内部井字形的两根水平横轴![]() 米,两根竖轴
米,两根竖轴![]() 米,记整个方舱医院的外围隔离线(图2实线部分,轴和边框的粗细忽略不计)总长度为
米,记整个方舱医院的外围隔离线(图2实线部分,轴和边框的粗细忽略不计)总长度为![]() ,
,![]() 与
与![]() 、
、![]() 的交点为
的交点为![]() 、
、![]() ,
,![]() 与
与![]() 、
、![]() 的交点为
的交点为![]() 、
、![]() ,
,![]() (
(![]() ).
).

(1)若![]() ,且两根横轴之间的距离
,且两根横轴之间的距离![]() 米,求外围隔离线总长度
米,求外围隔离线总长度![]() ;
;
(2)由于疫情需要,外围隔离线总长度![]() 不超过240米,当整个方舱医院(多边形
不超过240米,当整个方舱医院(多边形![]() 的面积)最大时,给出此设计方案中
的面积)最大时,给出此设计方案中![]() 的大小与
的大小与![]() 的长度.
的长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() ,把
,把![]() 上各点横坐标伸长为原来的2倍,纵坐标不变,得到函数
上各点横坐标伸长为原来的2倍,纵坐标不变,得到函数![]() 的图象,关于
的图象,关于![]() 有下述四个结论:
有下述四个结论:
(1)函数![]() 在
在![]() 上是减函数;
上是减函数;
(2)当![]() ,且
,且![]() 时,
时,![]() ,则
,则![]() ;
;
(3)函数![]() (其中
(其中![]() )的最小值为
)的最小值为![]() .
.
其中正确结论的个数为( ).
A.1B.2C.3D.0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用![]() 表示一个小于或等于
表示一个小于或等于![]() 的最大整数.如:
的最大整数.如:![]() ,
,![]() ,
,![]() . 已知实数列
. 已知实数列![]() 、
、![]() 、
、![]() 对于所有非负整数
对于所有非负整数![]() 满足
满足![]() ,其中
,其中![]() 是任意一个非零实数.
是任意一个非零实数.
(Ⅰ)若![]() ,写出
,写出![]() 、
、![]() 、
、![]() ;
;
(Ⅱ)若![]() ,求数列
,求数列![]() 的最小值;
的最小值;
(Ⅲ)证明:存在非负整数![]() ,使得当
,使得当![]() 时,
时,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 与
与![]() 轴正半轴交于点
轴正半轴交于点![]() ,与
,与![]() 轴交于
轴交于![]() 、
、![]() 两点.
两点.
(1)求过![]() 、
、![]() 、
、![]() 三点的圆
三点的圆![]() 的方程;
的方程;
(2)若![]() 为坐标原点,直线
为坐标原点,直线![]() 与椭圆
与椭圆![]() 和(1)中的圆
和(1)中的圆![]() 分别相切于点
分别相切于点![]() 和点
和点![]() (
(![]() 、
、![]() 不重合),求直线
不重合),求直线![]() 与直线
与直线![]() 的斜率之积.
的斜率之积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“熔喷布”是口罩生产的重要原材料,1吨熔喷布大约可供生产100万只口罩.2020年,制造口罩的企业甲的熔喷布1月份的需求量为100吨,并且从2月份起,每月熔喷布的需求量均比上个月增加10%.企业乙是企业甲熔喷布的唯一供应商,企业乙2020年1月份的产能为100吨,为满足市场需求,从2月份到![]() 月份(
月份(![]() 且
且![]() ),每个月比上个月增加一条月产量为50吨的生产线投入生产,从
),每个月比上个月增加一条月产量为50吨的生产线投入生产,从![]() 月份到9月份不再增加新的生产线.计划截止到9月份,企业乙熔喷布的总产量除供应企业甲的需求外,还剩余不少于990吨的熔喷布可供给其它厂商,则企业乙至少要增加___条熔喷布生产线.
月份到9月份不再增加新的生产线.计划截止到9月份,企业乙熔喷布的总产量除供应企业甲的需求外,还剩余不少于990吨的熔喷布可供给其它厂商,则企业乙至少要增加___条熔喷布生产线.
(参考数据:![]() ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某基地蔬菜大棚采用无土栽培方式种植各类蔬菜.根据过去50周的资料显示,该基地周光照量![]() (小时)都在30小时以上,其中不足50小时的有5周,不低于50小时且不超过70小时的有35周,超过70小时的有10周.根据统计,该基地的西红柿增加量
(小时)都在30小时以上,其中不足50小时的有5周,不低于50小时且不超过70小时的有35周,超过70小时的有10周.根据统计,该基地的西红柿增加量![]() (千克)与使用某种液体肥料的质量
(千克)与使用某种液体肥料的质量![]() (千克)之间的关系如图所示.
(千克)之间的关系如图所示.
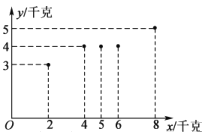
(1)依据上图,是否可用线性回归模型拟合![]() 与
与![]() 的关系?请计算相关系数
的关系?请计算相关系数![]() 并加以说明(精确到0.01).(若
并加以说明(精确到0.01).(若![]() ,则线性相关程度很高,可用线性回归模型拟合)
,则线性相关程度很高,可用线性回归模型拟合)
(2)蔬菜大棚对光照要求较大,某光照控制仪商家为该基地提供了部分光照控制仪,但每周光照控制仪运行台数受周光照量![]() 限制,并有如下关系:
限制,并有如下关系:
周光照量 |
|
|
|
光照控制仪运行台数 | 3 | 2 | 1 |
若某台光照控制仪运行,则该台光照控制仪周利润为3000元;若某台光照控制仪未运行,则该台光照控制仪周亏损1000元.以频率作为概率,商家欲使周总利润的均值达到最大,应安装光照控制仪多少台?
附:相关系数公式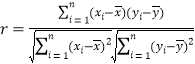 ,
,
参考数据:![]() ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com