
【题目】已知椭圆C :![]() 与圆
与圆![]() 相交于M,N,P,Q四点,四边形MNPQ为正方形,△PF1F2的周长为
相交于M,N,P,Q四点,四边形MNPQ为正方形,△PF1F2的周长为![]()
(1)求椭圆C的方程;
(2)设直线l与椭圆C相交于A、B两点![]() 若直线AD与直线BD的斜率之积为
若直线AD与直线BD的斜率之积为![]() ,证明:直线恒过定点.
,证明:直线恒过定点.
【答案】(1)![]() (2)见解析
(2)见解析
【解析】
(1)根据四边形MNPQ为正方形,可得到关于![]() 的一个方程,由△PF1F2的周长为
的一个方程,由△PF1F2的周长为![]() 得到关于
得到关于![]() 的另一个方程,联立方程,解方程组,即可得到椭圆C的方程.
的另一个方程,联立方程,解方程组,即可得到椭圆C的方程.
(2)对直线l的斜率存在与否进行讨论,当斜率不存在时,结合条件容易排除,当斜率存在时,设出直线方程与椭圆方程联立,得到两根之和、两根之积,将条件直线AD与直线BD的斜率之积为![]() 转化为韦达定理的形式,代入化简即可证明结论.
转化为韦达定理的形式,代入化简即可证明结论.
解:(1)
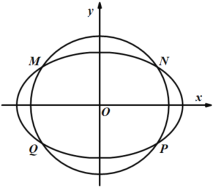
如图所示,设点![]() ,
,
由题意四边形MNPQ为正方形,所以![]() ,即
,即![]() ,
,
因为点![]() 在圆
在圆![]() 上,所以
上,所以![]() ,
,
即![]() ,又点
,又点![]() 在椭圆
在椭圆![]() 上,
上,
所以![]() ,即
,即![]() ,
,
所以![]() ①,
①,
又△PF1F2的周长为![]() ,
,
即![]() ②,
②,
由①②解得![]() ,
,![]() ,
,
所以椭圆![]() 的方程为:
的方程为:![]() .
.
(2)①当直线![]() 斜率不存在时,设
斜率不存在时,设![]() :
:![]() ,
,![]() ,
,![]() ,
,
因为点![]() 在椭圆
在椭圆![]() 上,
上,
所以![]() ,即
,即![]() ,
,
所以![]()
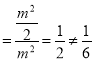 不满足题意.
不满足题意.
②当直线![]() 斜率存在时,设
斜率存在时,设![]() :
:![]() ,
,
![]() ,
,![]() ,联立
,联立![]() ,
,
整理得![]() ,
,
所以![]() ,
,![]() ,
,
则![]()
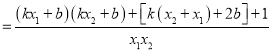
![]() ,
,
将![]() ,
,![]() 代入上式化简得:
代入上式化简得:
![]()
![]() .
.
即![]() ,解得,
,解得,![]() ,
,
所以直线![]() 恒过定点
恒过定点![]() .
.


 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:高中数学 来源: 题型:
【题目】设无穷数列![]() 的每一项均为正数,对于给定的正整数
的每一项均为正数,对于给定的正整数![]() ,
,![]() (
(![]() ),若
),若![]() 是等比数列,则称
是等比数列,则称![]() 为
为![]() 数列.
数列.
(1)求证:若![]() 是无穷等比数列,则
是无穷等比数列,则![]() 是
是![]() 数列;
数列;
(2)请你写出一个不是等比数列的![]() 数列的通项公式;
数列的通项公式;
(3)设![]() 为
为![]() 数列,且满足
数列,且满足![]() ,请用数学归纳法证明:
,请用数学归纳法证明:![]() 是等比数列.
是等比数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有关部门在某公交站点随机抽取了100名乘客,统计其乘车等待时间(指乘客从进站口到乘上车的时间,乘车等待时间不超过40分钟),将数据按![]() ,
,![]() ,
,![]() ,
,![]()
![]() ,
,![]() ,
,![]() 分组,绘制成如图所示的频率分布直方图.
分组,绘制成如图所示的频率分布直方图.
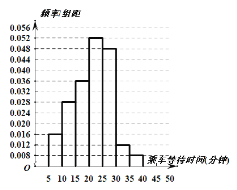
假设乘客乘车等待时间相互独立.
(1)求抽取的100名乘客乘车等待时间的中位数(保留一位小数);
(2)现从该车站等车的乘客中随机抽取4人,记等车时间在![]() 的人数为
的人数为![]() ,用频率估计概率,求随机变量
,用频率估计概率,求随机变量![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为等差数列,各项为正的等比数列
为等差数列,各项为正的等比数列![]() 的前n项和为
的前n项和为![]() , ,且
, ,且![]() ,
,![]() ,.在①
,.在①![]() ;②
;②![]() ;③
;③![]() 这三个条件中任选其中一个,补充在上面的横线上,并完成下面问题的解答(如果选择多个条件解答,则按选择第一个解答计分).
这三个条件中任选其中一个,补充在上面的横线上,并完成下面问题的解答(如果选择多个条件解答,则按选择第一个解答计分).
(1)求数列![]() 和
和![]() 的通项公式;
的通项公式;
(2)求数列![]() 的前
的前![]() 项和
项和![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】抛物线![]() 的焦点为F,P为其上一动点,设直线l与抛物线C相交于A,B两点,点
的焦点为F,P为其上一动点,设直线l与抛物线C相交于A,B两点,点![]() 下列结论正确的是( )
下列结论正确的是( )
A.|PM| +|PF|的最小值为3
B.抛物线C上的动点到点![]() 的距离最小值为3
的距离最小值为3
C.存在直线l,使得A,B两点关于![]() 对称
对称
D.若过A、B的抛物线的两条切线交准线于点T,则A、B两点的纵坐标之和最小值为2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】方舱医院的启用在本次武汉抗击新冠疫情的关键时刻起到了至关重要的作用,图1为某方舱医院的平面设计图,其结构可以看成矩形在四个角处对称地截去四个全等的三角形所得,图2中所示多边形![]() ,整体设计方案要求:内部井字形的两根水平横轴
,整体设计方案要求:内部井字形的两根水平横轴![]() 米,两根竖轴
米,两根竖轴![]() 米,记整个方舱医院的外围隔离线(图2实线部分,轴和边框的粗细忽略不计)总长度为
米,记整个方舱医院的外围隔离线(图2实线部分,轴和边框的粗细忽略不计)总长度为![]() ,
,![]() 与
与![]() 、
、![]() 的交点为
的交点为![]() 、
、![]() ,
,![]() 与
与![]() 、
、![]() 的交点为
的交点为![]() 、
、![]() ,
,![]() (
(![]() ).
).

(1)若![]() ,且两根横轴之间的距离
,且两根横轴之间的距离![]() 米,求外围隔离线总长度
米,求外围隔离线总长度![]() ;
;
(2)由于疫情需要,外围隔离线总长度![]() 不超过240米,当整个方舱医院(多边形
不超过240米,当整个方舱医院(多边形![]() 的面积)最大时,给出此设计方案中
的面积)最大时,给出此设计方案中![]() 的大小与
的大小与![]() 的长度.
的长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() ,把
,把![]() 上各点横坐标伸长为原来的2倍,纵坐标不变,得到函数
上各点横坐标伸长为原来的2倍,纵坐标不变,得到函数![]() 的图象,关于
的图象,关于![]() 有下述四个结论:
有下述四个结论:
(1)函数![]() 在
在![]() 上是减函数;
上是减函数;
(2)当![]() ,且
,且![]() 时,
时,![]() ,则
,则![]() ;
;
(3)函数![]() (其中
(其中![]() )的最小值为
)的最小值为![]() .
.
其中正确结论的个数为( ).
A.1B.2C.3D.0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 与
与![]() 轴正半轴交于点
轴正半轴交于点![]() ,与
,与![]() 轴交于
轴交于![]() 、
、![]() 两点.
两点.
(1)求过![]() 、
、![]() 、
、![]() 三点的圆
三点的圆![]() 的方程;
的方程;
(2)若![]() 为坐标原点,直线
为坐标原点,直线![]() 与椭圆
与椭圆![]() 和(1)中的圆
和(1)中的圆![]() 分别相切于点
分别相切于点![]() 和点
和点![]() (
(![]() 、
、![]() 不重合),求直线
不重合),求直线![]() 与直线
与直线![]() 的斜率之积.
的斜率之积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)函数![]() ,讨论
,讨论![]() 的单调性;
的单调性;
(2)曲线![]() 在点
在点![]() 处的切线为
处的切线为![]() ,是否存在这样的点
,是否存在这样的点![]() 使得直线
使得直线![]() 与曲线
与曲线![]() 也相切,若存在,判断满足条件的点
也相切,若存在,判断满足条件的点![]() 的个数,若不存在,请说明理由.
的个数,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com