
【题目】设无穷数列![]() 的每一项均为正数,对于给定的正整数
的每一项均为正数,对于给定的正整数![]() ,
,![]() (
(![]() ),若
),若![]() 是等比数列,则称
是等比数列,则称![]() 为
为![]() 数列.
数列.
(1)求证:若![]() 是无穷等比数列,则
是无穷等比数列,则![]() 是
是![]() 数列;
数列;
(2)请你写出一个不是等比数列的![]() 数列的通项公式;
数列的通项公式;
(3)设![]() 为
为![]() 数列,且满足
数列,且满足![]() ,请用数学归纳法证明:
,请用数学归纳法证明:![]() 是等比数列.
是等比数列.
【答案】(1)证明见解析.(2)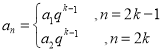 (
(![]() ).(答案不唯一).(3)证明见解析
).(答案不唯一).(3)证明见解析
【解析】
(1)通过证明![]() ,证得数列
,证得数列![]() 是等比数列,由此证得
是等比数列,由此证得![]() 为
为![]() 数列.
数列.
(2)根据满足![]() 的数列
的数列![]() 是等比数列,但无穷数列
是等比数列,但无穷数列![]() 不是等比数列,举出相应的例子.
不是等比数列,举出相应的例子.
(3)首先根据已知条件得到![]() ,再利用数学归纳法证明
,再利用数学归纳法证明![]() (或者利用数学归纳法证明
(或者利用数学归纳法证明![]() ),由此证得
),由此证得![]() 是等比数列.
是等比数列.
(1)设![]() 是公比为
是公比为![]() 的等比数列,对于给定的正整数
的等比数列,对于给定的正整数![]() ,
,![]() (
(![]() ),
),
∴![]() ,
,![]() ,
,
又![]() ,∴
,∴![]() 是等比数列,
是等比数列,
∴![]() 为
为![]() 数列.
数列.
(2)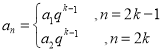 (
(![]() ).(答案不唯一)
).(答案不唯一)
简洁的例子如:![]() (
(![]() ).
).
(3)∵![]() 为
为![]() 数列,∴
数列,∴![]() 是等比数列,其中
是等比数列,其中![]() (
(![]() ),
),
∴![]() (
(![]() ),
),
∴![]() (
(![]() )是常数列,设常数为
)是常数列,设常数为![]() ,即
,即![]() (
(![]() ),
),
以下用数学归纳法证明(法一)![]() (
(![]() ),
),
①由已知![]() 可得:当
可得:当![]() 时命题成立;
时命题成立;
②假设![]() (
(![]() ,
,![]() )时命题成立,即,
)时命题成立,即,![]() ,
,
当![]() 时,∵
时,∵![]() (
(![]() )是常数列,
)是常数列,
∴![]() (
(![]() ,
,![]() ),
),
∴![]() ,
,
等式也成立.
根据①和②可以断定,![]() 对任何
对任何![]() 都成立,即
都成立,即![]() 是等比数列.
是等比数列.
令![]() ,以下用数学归纳法证明(法二)
,以下用数学归纳法证明(法二)![]() (
(![]() ),
),
①∵![]() ,∴
,∴![]() ,∴
,∴![]() ,∴
,∴![]() ,即
,即![]() ,
,
∴当![]() 时命题成立,
时命题成立,
假设![]() (
(![]() ,
,![]() )时命题成立,即
)时命题成立,即![]() (
(![]() );
);
②当![]() 时,
时,![]() ,
,
等式也成立;
根据①和②可以断定,![]() 对任何
对任何![]() 都成立,即
都成立,即![]() 是等比数列.
是等比数列.


科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为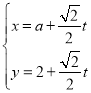 (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 和曲线
和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若点![]() 坐标为
坐标为![]() ,直线
,直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,且
两点,且![]() ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂计划建设至少3个,至多5个相同的生产线车间,以解决本地区公民对特供商品![]() 的未来需求.经过对先期样本的科学性调查显示,本地区每个月对商品
的未来需求.经过对先期样本的科学性调查显示,本地区每个月对商品![]() 的月需求量均在50万件及以上,其中需求量在50~ 100万件的频率为0.5,需求量在100~200万件的频率为0.3,不低于200万件的频率为0.2.用调查样本来估计总体,频率作为相应段的概率,并假设本地区在各个月对本特供商品
的月需求量均在50万件及以上,其中需求量在50~ 100万件的频率为0.5,需求量在100~200万件的频率为0.3,不低于200万件的频率为0.2.用调查样本来估计总体,频率作为相应段的概率,并假设本地区在各个月对本特供商品![]() 的需求相互独立.
的需求相互独立.
(1)求在未来某连续4个月中,本地区至少有2个月对商品![]() 的月需求量低于100万件的概率.
的月需求量低于100万件的概率.
(2)该工厂希望尽可能在生产线车间建成后,车间能正常生产运行,但每月最多可正常生产的车间数受商品![]() 的需求量
的需求量![]() 的限制,并有如下关系:
的限制,并有如下关系:
商品 |
|
|
|
车间最多正常运行个数 | 3 | 4 | 5 |
若一个车间正常运行,则该车间月净利润为1500万元,而一个车间未正常生产,则该车间生产线的月维护费(单位:万元)与月需求量有如下关系:
商品 |
|
|
未正常生产的一个车间的月维护费(万元) | 500 | 600 |
试分析并回答该工厂应建设生产线车间多少个?使得商品![]() 的月利润为最大.
的月利润为最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ,直线
,直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,
两点,![]() 为坐标原点.
为坐标原点.
(1)若直线![]() 过椭圆
过椭圆![]() 的右焦点
的右焦点![]() ,求
,求![]() 的面积;
的面积;
(2)椭圆![]() 上是否存在点
上是否存在点![]() ,使得四边形
,使得四边形![]() 为平行四边形?若存在,求出所有满足条件的
为平行四边形?若存在,求出所有满足条件的![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国古代几何中的勾股容圆,是阐述直角三角形中内切圆问题. 此类问题最早见于《九章算术》“勾股”章,该章第16题为:“今有勾八步,股十五步. 问勾中容圆,径几何?”意思是“直角三角形的两条直角边分别为8和15,则其内切圆直径是多少?”若向上述直角三角形内随机抛掷120颗米粒(大小忽略不计,取![]() ),落在三角形内切圆内的米粒数大约为( )
),落在三角形内切圆内的米粒数大约为( )
A.54B.48C.42D.36
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年,新型冠状病毒引发的疫情牵动着亿万人的心,八方驰援战疫情,众志成城克时难,社会各界支援湖北共抗新型冠状病毒肺炎,重庆某医院派出3名医生,2名护士支援湖北,现从这5人中任选2人定点支援湖北某医院,则恰有1名医生和1名护士被选中的概率为( )
A.0.7B.0.4C.0.6D.0.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】南宋数学家杨辉在《详解九章算法》和《算法通变本末》中,提出了一些新的垛积公式,所讨论的高阶等差数列与一般等差数列不同,前后两项之差并不相等,但是逐项差数之差或者高次差成等差数列.对这类高阶等差数列的研究,在杨辉之后一般称为“垛积术”.现有高阶等差数列,其前7项分别为1,5,11,21,37,6l,95,则该数列的第8项为( )
A.99B.131C.139D.141
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C :![]() 与圆
与圆![]() 相交于M,N,P,Q四点,四边形MNPQ为正方形,△PF1F2的周长为
相交于M,N,P,Q四点,四边形MNPQ为正方形,△PF1F2的周长为![]()
(1)求椭圆C的方程;
(2)设直线l与椭圆C相交于A、B两点![]() 若直线AD与直线BD的斜率之积为
若直线AD与直线BD的斜率之积为![]() ,证明:直线恒过定点.
,证明:直线恒过定点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com