【题目】已知椭圆的离心率，椭圆上的点到其左焦点的最大距离为．

（1）求椭圆的标准方程；

（2）过椭圆左焦点的直线与椭圆交于两点，直线，过点作直线的垂线与直线交于点，求的最小值和此时直线的方程．

【题目】某工厂生产某种电子产品，每件产品合格的概率均为，现工厂为提高产品声誉，要求在交付用户前每件产品都通过合格检验，已知该工厂的检验仪器一次最多可检验件该产品，且每件产品检验合格与否相互独立．若每件产品均检验一次，所需检验费用较多，该工厂提出以下检验方案：将产品每个（）一组进行分组检验，如果某一组产品检验合格，则说明该组内产品均合格，若检验不合格，则说明该组内有不合格产品，再对该组内每一件产品单独进行检验，如此，每一组产品只需检验一次或次．设该工厂生产件该产品，记每件产品的平均检验次数为．

（1）的分布列及其期望；

（2）（i）试说明，当越大时，该方案越合理，即所需平均检验次数越少；

（ii）当时，求使该方案最合理时的值及件该产品的平均检验次数．

【题目】波罗尼斯（古希腊数学家，约公元前262-190年）的著作《圆锥曲线论》是古代世界光辉的科学成果，它将圆锥曲线的性质网罗殆尽几乎使后人没有插足的余地.他证明过这样一个命题：平面内与两定点距离的比为常数k（且）的点的轨迹是圆，后人将这个圆称为阿波罗尼斯圆.现有，，则当的面积最大时，AC边上的高为_______________.

【题目】《周易》是我国古代典籍，用“卦”描述了天地世间万象变化．如图是一个八卦图，包含乾、坤、震、巽、坎、离、艮、兑八卦（每一卦由三个爻组成，其中“”表示一个阳爻，“”表示一个阴爻）．若从八卦中任取两卦，这两卦的六个爻中恰有一个阳爻的概率为（ ）

A.B.

C.D.

【题目】已知数列的前项和为，把满足条件（对任意的）的所有数列构成的集合记为.

（1）若数列的通项为，判断是否属于，并说明理由；

（2）若数列的通项为，判断是否属于，并说明理由；

（3）若数列是等差数列，且，求的取值范围.

【题目】已知椭圆（）的右焦点为，左右顶点分别为、，，过点的直线（不与轴重合）交椭圆于、点，直线与轴的交点为，与直线的交点为.

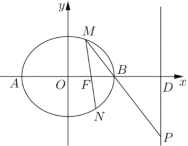
（1）求椭圆的方程；

（2）若，求出点的坐标；

（3）求证：、、三点共线.

【题目】如图，在郊野公园的景观河的两岸，、是夹角为120°的两条岸边步道（长度均超过千米），为方便市民观光游览，现准备在河道拐角处的另一侧建造一个观景台，在两条步道、上分别设立游客上下点、，从、到观景台建造两条游船观光线路、，测得千米.

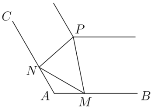
（1）求游客上下点、间的距离；

（2）若，设，求两条观光线路与之和关于的表达式，并求其最大值.

【题目】2021年某省将实行“”的新高考模式，即语文、数学、英语三科必选，物理、历史二选一，化学、生物、政治、地理四选二，若甲同学选科没有偏好，且不受其他因素影响，则甲同学同时选择历史和化学的概率为________

【题目】已知圆C方程为，椭圆中心在原点，焦点在x轴上.

（1）证明圆C恒过一定点M，并求此定点M的坐标；

（2）判断直线与圆C的位置关系，并证明你的结论；

（3）当时，圆C与椭圆的左准线相切，且椭圆过（1）中的点M，求此时椭圆方程；在x轴上是否存在两定点A，B使得对椭圆上任意一点Q（异于长轴端点），直线，的斜率之积为定值？若存在，求出A，B坐标；若不存在，请说明理由.

【题目】设数列的各项均为不等的正整数，其前项和为，我们称满足条件“对任意的，均有”的数列为“好”数列．

（1）试分别判断数列，是否为“好”数列，其中，，，并给出证明；

（2）已知数列为“好”数列．

① 若，求数列的通项公式；

② 若，且对任意给定正整数（），有成等比数列，求证：．