【题目】若存在常数，使对任意的，都有，则称数列为数列.

（1）已知是公差为2的等差数列，其前n项和为.若是数列，求的取值范围；

（2）已知数列的各项均为正数，记数列的前n项和为，数列的前n项和为，且.

①求证：数列是等比数列；

②设，试证明：存在常数，对于任意的，数列都是数列.

【题目】已知函数.

（1）若是函数的极值点，求a的值；

（2）令，若对任意，有恒成立，求a的取值范围；

（3）设m，n为实数，且，求证：.

【题目】在平面直角坐标系xOy中，已知椭圆经过，且右焦点坐标为.

（1）求椭圆的标准方程；

（2）设A，B为椭圆的左，右顶点，C为椭圆的上顶点，P为椭圆上任意一点（异于A，B两点），直线AC与直线BP相交于点M，直线BC与直线AP相交于点N，求证：.

【题目】如图，海岸公路MN的北方有一个小岛A（大小忽略不计）盛产海产品，在公路MN的B处有一个海产品集散中心，点C在B的正西方向10处，，，计划开辟一条运输线将小岛的海产品运送到集散中心.现有两种方案：①沿线段AB开辟海上航线：②在海岸公路MN上选一点P建一个码头，先从海上运到码头，再公路MN运送到集散中心.已知海上运输、岸上运输费用分别为400元/、200元/.

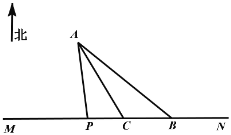
（1）求方案①的运输费用；

（2）请确定P点的位置，使得按方案②运送时运输费用最低？

【题目】如图，在四棱柱ABCD-A1B1C1D1中，ABCD，AB1⊥BC，且AA1＝AB.求证：

（1）AB平面D1DCC1；

（2）AB1⊥平面A1BC.

（1）|a|+|b+c﹣1|；

（2）（a3+b3+c3）（）≥3.

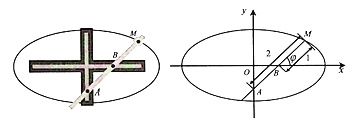
（1）将以射线Bx为始边，射线BM为终边的角xBM记为φ（0≤φ＜2π），用表示点M的坐标，并求出C的普通方程；

（2）已知过C的左焦点F，且倾斜角为α（0≤α）的直线l1与C交于D，E两点，过点F且垂直于l1的直线l2与C交于G，H两点.当，|GH|，依次成等差数列时，求直线l2的普通方程.

【题目】已知函数．（其中常数，是自然对数的底数）

（1）若，求在上的极大值点；

（2）（）证明在上单调递增；

（）求关于的方程在上的实数解的个数．

【题目】在平面直角坐标系中，P为直线：上的动点，动点Q满足，且原点O在以为直径的圆上.记动点Q的轨迹为曲线C

（1）求曲线C的方程：

（2）过点的直线与曲线C交于A，B两点，点D（异于A，B）在C上，直线，分别与x轴交于点M，N，且，求面积的最小值.

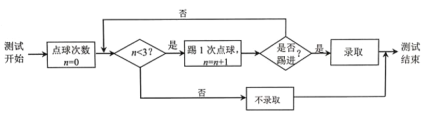
（1）下表是某同学6次的训练数据，以这150个点球中的进球频率代表其单次点球踢进的概率.为加入足球社团，该同学进行了“点球测试”，每次点球是否踢进相互独立，将他在测试中所踢的点球次数记为，求；

（2）社团中的甲、乙、丙三名成员将进行传球训练，从甲开始随机地将球传给其他两人中的任意一人，接球者再随机地将球传给其他两人中的任意一人，如此不停地传下去，且假定每次传球都能被接到.记开始传球的人为第1次触球者，接到第n次传球的人即为第次触球者，第n次触球者是甲的概率记为.

（i）求，，（直接写出结果即可）；

（ii）证明：数列为等比数列.