
科目: 来源: 题型:
【题目】定义在![]() 上的函数
上的函数![]() 若满足:①对任意
若满足:①对任意![]() 、
、![]() ,都有
,都有![]() ;②对任意
;②对任意![]() ,都有
,都有![]() ,则称函数
,则称函数![]() 为“中心捺函数”,其中点
为“中心捺函数”,其中点![]() 称为函数
称为函数![]() 的中心.已知函数
的中心.已知函数![]() 是以
是以![]() 为中心的“中心捺函数”,若满足不等式
为中心的“中心捺函数”,若满足不等式![]() ,当
,当![]() 时,
时,![]() 的取值范围为( )
的取值范围为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】对于数列![]() ,若对任意的
,若对任意的![]() ,
,![]() 也是数列
也是数列![]() 中的项,则称数列
中的项,则称数列![]() 为“
为“![]() 数列”,已知数列
数列”,已知数列![]() 满足:对任意的
满足:对任意的![]() ,均有
,均有![]() ,其中
,其中![]() 表示数列
表示数列![]() 的前
的前![]() 项和.
项和.
(1)求证:数列![]() 为等差数列;
为等差数列;
(2)若数列![]() 为“
为“![]() 数列”,
数列”,![]() ,
,![]() 且
且![]() ,求
,求![]() 的所有可能值;
的所有可能值;
(3)若对任意的![]() ,
,![]() 也是数列
也是数列![]() 中的项,求证:数列
中的项,求证:数列![]() 为“
为“![]() 数列”.
数列”.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() 的方程为
的方程为![]() ,圆
,圆![]() 与
与![]() 轴相切于点
轴相切于点![]() ,与
,与![]() 轴正半轴相交于
轴正半轴相交于![]() 、
、![]() 两点,且
两点,且![]() ,如图1.
,如图1.
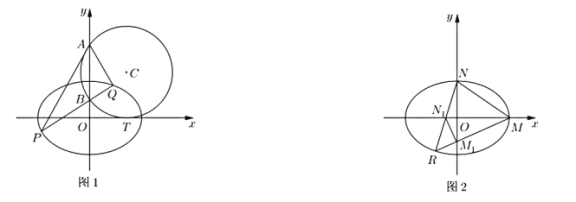
(1)求圆![]() 的方程;
的方程;
(2)如图1,过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 、
、![]() 两点,求证:射线
两点,求证:射线![]() 平分
平分![]() ;
;
(3)如图2所示,点![]() 、
、![]() 是椭圆
是椭圆![]() 的两个顶点,且第三象限的动点
的两个顶点,且第三象限的动点![]() 在椭圆
在椭圆![]() 上,若直线
上,若直线![]() 与
与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,试问:四边形
,试问:四边形![]() 的面积是否为定值?若是,请求出这个定值,若不是,请说明理由.
的面积是否为定值?若是,请求出这个定值,若不是,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
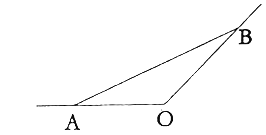
【题目】如图所示,某城市有一条从正西方AO通过市中心O后向东北OB的公路,现要修一条地铁L,在OA,OB上各设一站A,B,地铁在AB部分为直线段,现要求市中心O与AB的距离为![]() ,设地铁在AB部分的总长度为
,设地铁在AB部分的总长度为![]() .
.
![]() 按下列要求建立关系式:
按下列要求建立关系式:
![]() 设
设![]() ,将y表示成
,将y表示成![]() 的函数;
的函数;
![]() 设
设![]() ,
,![]() 用m,n表示y.
用m,n表示y.
![]() 把A,B两站分别设在公路上离中心O多远处,才能使AB最短?并求出最短距离.
把A,B两站分别设在公路上离中心O多远处,才能使AB最短?并求出最短距离.
查看答案和解析>>
科目: 来源: 题型:
【题目】在某次测验中,某班40名考生的成绩满分100分统计如图所示.

(Ⅰ)估计这40名学生的测验成绩的中位数![]() 精确到0.1;
精确到0.1;
(Ⅱ)记80分以上为优秀,80分及以下为合格,结合频率分布直方图完成下表,并判断是否有95%的把握认为数学测验成绩与性别有关?
合格 | 优秀 | 合计 | |
男生 | 16 | ||
女生 | 4 | ||
合计 | 40 |
附:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】设椭圆![]() 的右顶点为A,下顶点为B,过A、O、B(O为坐标原点)三点的圆的圆心坐标为
的右顶点为A,下顶点为B,过A、O、B(O为坐标原点)三点的圆的圆心坐标为![]() .
.
(1)求椭圆的方程;
(2)已知点M在x轴正半轴上,过点B作BM的垂线与椭圆交于另一点N,若∠BMN=60°,求点M的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】【2018届北京市海淀区】如图,三棱柱![]() 侧面
侧面![]() 底面
底面![]() ,
, ![]()
![]()
![]() ,
, ![]() 分别为棱
分别为棱![]() 的中点.
的中点.
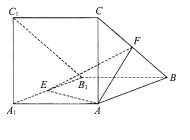
(Ⅰ)求证: ![]() ;
;
(Ⅱ)求三棱柱![]() 的体积;
的体积;
(Ⅲ)在直线![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的长;若不存在,说明理由.
的长;若不存在,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】我国古代科学家祖冲之儿子祖暅在实践的基础上提出了体积计算的原理:“幂势既同,则积不容异”(“幂”是截面积,“势”是几何体的高),意思是两个同高的几何体,如在等高处截面的面积恒相等,则它们的体积相等.已知某不规则几何体与如图所示的三视图所表示的几何体满足“幂势既同”,则该不规则几何体的体积为( )
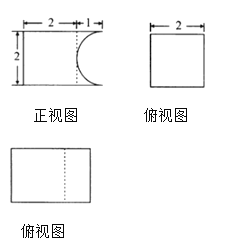
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】已知极点为直角坐标系的原点,极轴为![]() 轴正半轴且单位长度相同的极坐标系中曲线
轴正半轴且单位长度相同的极坐标系中曲线![]() ,
,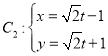 (
(![]() 为参数).
为参数).
(Ⅰ)求曲线![]() 上的点到曲线
上的点到曲线![]() 距离的最小值;
距离的最小值;
(Ⅱ)若把![]() 上各点的横坐标都扩大原来为原来的2倍,纵坐标扩大原来的
上各点的横坐标都扩大原来为原来的2倍,纵坐标扩大原来的![]() 倍,得到曲线
倍,得到曲线![]() ,设
,设![]() ,曲线
,曲线![]() 与
与![]() 交于
交于![]() ,
,![]() 两点,求
两点,求![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com