
科目: 来源: 题型:
【题目】已知直线![]() 经过椭圆
经过椭圆![]() :
: ![]() 的左顶点
的左顶点![]() 和上顶点
和上顶点![]() ,椭圆
,椭圆![]() 的右顶点为
的右顶点为![]() ,点
,点![]() 是椭圆
是椭圆![]() 上位于
上位于![]() 轴上方的动点,直线
轴上方的动点,直线![]() 与直线
与直线![]() 分别交于
分别交于![]() 两点。
两点。
(1)求椭圆方程;
(2)求线段![]() 的长度的最小值;
的长度的最小值;
(3)当线段![]() 的长度最小时,在椭圆上有两点
的长度最小时,在椭圆上有两点![]() ,使得
,使得![]() ,
,![]() 的面积都为
的面积都为![]() ,求直线
,求直线![]() 在y轴上的截距。
在y轴上的截距。
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知等腰梯形![]() 中,
中,![]() 是
是![]() 的中点,
的中点,![]()
![]() ,将
,将![]() 沿着
沿着![]() 翻折成
翻折成![]() ,使平面
,使平面![]() 平面
平面![]() .
.


(Ⅰ)求证:![]() ;
;
(Ⅱ)求二面角![]() 的余弦值;
的余弦值;
(Ⅲ)在线段![]() 上是否存在点P,使得
上是否存在点P,使得![]() 平面
平面![]() ,若存在,求出
,若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() (
(![]() ,
,![]() 是自然对数的底数).
是自然对数的底数).
(1)若函数![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() ,试确定函数
,试确定函数![]() 的单调区间;
的单调区间;
(2)①当![]() ,
,![]() 时,若对于任意
时,若对于任意![]() ,都有
,都有![]() 恒成立,求实数
恒成立,求实数![]() 的最小值;②当
的最小值;②当![]() 时,设函数
时,设函数![]() ,是否存在实数
,是否存在实数![]() ,使得
,使得![]() ?若存在,求出
?若存在,求出![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】2018年森林城市建设座谈会在深圳举行.会上宣读了国家森林城市称号批准决定,并举行授牌仪式,滕州市榜上有名,被正式批准为“国家森林城市”.为进一步推进国家森林城市建设,我市准备制定生态环境改造投资方案,该方案要求同时具备下列两个条件:
①每年用于风景区改造的费用![]() 随每年改造生态环境总费用
随每年改造生态环境总费用![]() 增加而增加;②每年用于风景区改造的费用
增加而增加;②每年用于风景区改造的费用![]() 不得低于每年改造生态环境总费用
不得低于每年改造生态环境总费用![]() 的15%,但不得高于每年改造生态环境总费用
的15%,但不得高于每年改造生态环境总费用![]() 的25%.若每年改造生态环境的总费用至少1亿元,至多4亿元;请你分析能否采用函数模型
的25%.若每年改造生态环境的总费用至少1亿元,至多4亿元;请你分析能否采用函数模型![]() 作为生态环境改造投资方案.
作为生态环境改造投资方案.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() ,
,![]() (其中a是常数).
(其中a是常数).
(1)求过点![]() 与曲线
与曲线![]() 相切的直线方程;
相切的直线方程;
(2)是否存在![]() 的实数,使得只有唯一的正数a,当
的实数,使得只有唯一的正数a,当![]() 时不等式
时不等式![]() 恒成立,若这样的实数k存在,试求k,a的值;若不存在.请说明理由.
恒成立,若这样的实数k存在,试求k,a的值;若不存在.请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知BD为圆锥AO底面的直径,若![]() ,C是圆锥底面所在平面内一点,
,C是圆锥底面所在平面内一点,![]() ,且AC与圆锥底面所成角的正弦值为
,且AC与圆锥底面所成角的正弦值为![]() .
.
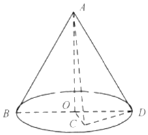
(1)求证:平面![]() 平面ACD;
平面ACD;
(2)求二面角![]() 的平面角的余弦值.
的平面角的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com