
科目: 来源: 题型:
【题目】已知等比数列![]() 的前n项和为
的前n项和为![]() ,且当
,且当![]() 时,
时,![]() 是
是![]() 与2m的等差中项
与2m的等差中项![]() 为实数
为实数![]() .
.
(1)求m的值及数列![]() 的通项公式;
的通项公式;
(2)令![]() ,是否存在正整数k,使得
,是否存在正整数k,使得![]() 对任意正整数n均成立?若存在,求出k的最大值;若不存在,说明理由.
对任意正整数n均成立?若存在,求出k的最大值;若不存在,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】党的十九大报告指出,在全面建成小康社会的决胜阶段,让贫困地区同全国人民共同进入全面小康社会是我们党的庄严承诺.在“脱真贫、真脱贫”的过程中,精准扶贫助推社会公平显得尤其重要.若某地区有100户贫困户,经过一年扶贫后,为了考查该地区的“精准扶贫”的成效![]() 该地区脱贫标准为“每户人均年收入不少于4000元”
该地区脱贫标准为“每户人均年收入不少于4000元”![]() ,现从该地区随机抽取A、B两个村庄,再从这两个村庄的贫困户中随机抽取20户,调查每户的现人均年收入,绘制如图所示的茎叶图
,现从该地区随机抽取A、B两个村庄,再从这两个村庄的贫困户中随机抽取20户,调查每户的现人均年收入,绘制如图所示的茎叶图![]() 单位:百元
单位:百元![]() .
.
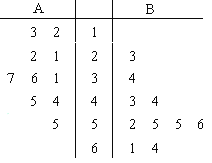
(1)观察茎叶图中的数据,判断哪个村庄扶贫成效较好?并说明理由;
(2)计划对没有脱贫的贫困户进一步实行“精准扶贫”,下一年的资金投入方案如下:对人均年收入不高于2000元的贫困户,每户每年增加扶贫资金5000元;对人均年收入高于2000元但不高于3000元的贫困户,每户每年增加扶贫资金3000元;对人均年收入高于3000元但不高于4000元的贫困户,每户每年增加扶贫资金1000元;对已经脱贫的贫困户不再增加扶贫资金投入.依据此方案,试估计下一年该地区共需要增加扶贫资金多少元?
查看答案和解析>>
科目: 来源: 题型:
【题目】![]() 九章算术
九章算术![]() 中对一些特殊的几何体有特定的称谓,例如:将底面为直角三角形的直三棱柱称为堑堵,将一堑堵沿其一顶点与相对的棱刨开,得到一个阳马
中对一些特殊的几何体有特定的称谓,例如:将底面为直角三角形的直三棱柱称为堑堵,将一堑堵沿其一顶点与相对的棱刨开,得到一个阳马![]() 底面是长方形,且有一条侧棱与底面垂直的四棱锥
底面是长方形,且有一条侧棱与底面垂直的四棱锥![]() 和一个鳖臑
和一个鳖臑![]() 四个面均为直角三角形的四面体
四个面均为直角三角形的四面体![]() 在如图所示的堑堵
在如图所示的堑堵![]() 中,已知
中,已知![]() ,若阳马
,若阳马![]() 的外接球的表面积等于
的外接球的表面积等于![]() ,则鳖臑
,则鳖臑![]() 的所有棱中,最长的棱的棱长为( )
的所有棱中,最长的棱的棱长为( )

A.5B.![]() C.
C.![]() D.8
D.8
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]()
![]() 的左、右焦点分别为
的左、右焦点分别为![]()
![]()
![]() ,过点
,过点![]() 且斜率为
且斜率为![]() 的直线和以椭圆的右顶点为圆心,短半轴为半径的圆相切.
的直线和以椭圆的右顶点为圆心,短半轴为半径的圆相切.
(1)求椭圆的方程;
(2)椭圆的左、右顶点分为A,B,过右焦点![]() 的直线l交椭圆于P,Q两点,求四边形APBQ面积的最大值.
的直线l交椭圆于P,Q两点,求四边形APBQ面积的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知四棱锥P-ABCD中,底面ABCD为直角梯形,![]() 平面ABCD,且
平面ABCD,且![]()
![]()
![]()
![]() .
.
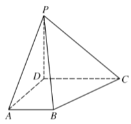
(1)求证:![]() 平面PBD;
平面PBD;
(2)若PB与平面ABCD所成的角为![]() ,求二面角D-PC-B的余弦值.
,求二面角D-PC-B的余弦值.
查看答案和解析>>
科目: 来源: 题型:
【题目】高三学生为了迎接高考,要经常进行模拟考试,锻炼应试能力,某学生从升入高三到高考要参加10次模拟考试,下面是高三第一学期某学生参加5次模拟考试的数学成绩表:
模拟考试第x次 | 1 | 2 | 3 | 4 | 5 |
考试成绩y分 | 90 | 100 | 105 | 105 | 100 |
(1)已知该考生的模拟考试成绩y与模拟考试的次数x满足回归直线方程![]() ,若高考看作第11次模拟考试,试估计该考生的高考数学成绩;
,若高考看作第11次模拟考试,试估计该考生的高考数学成绩;
(2)把这5次模拟考试的数学成绩单放在5个相同的信封中,从中随机抽取3份试卷的成绩单进行研究,设抽取考试成绩不等于平均值![]() 的个数为
的个数为![]() ,求出
,求出![]() 的分布列与数学期望.
的分布列与数学期望.
参考公式:
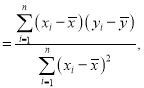
![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知正项数列![]() ,
,![]() 满足:对任意正整数
满足:对任意正整数![]() ,都有
,都有![]() ,
,![]() ,
,![]() 成等差数列,
成等差数列,![]() ,
,![]() ,
,![]() 成等比数列,且
成等比数列,且![]() ,
,![]() .
.
(Ⅰ)求证:数列![]() 是等差数列;
是等差数列;
(Ⅱ)求数列![]() ,
,![]() 的通项公式;
的通项公式;
(Ⅲ)设![]() =
=![]() +
+![]() +…+
+…+![]() ,如果对任意的正整数
,如果对任意的正整数![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】定义在![]() 上的函数
上的函数![]() ,如果满足:对任意
,如果满足:对任意![]() ,存在常数
,存在常数![]() ,都有
,都有![]() 成立,则称
成立,则称![]() 是
是![]() 上的有界函数,其中
上的有界函数,其中![]() 称为函数
称为函数![]() 的上界.
的上界.
(1)设![]() ,判断
,判断![]() 在
在![]() 上是否为有界函数,若是,请说明理由,并写出
上是否为有界函数,若是,请说明理由,并写出![]() 的所有上界
的所有上界![]() 的集合;若不是,也请说明理由;
的集合;若不是,也请说明理由;
(2)若函数![]() 在
在![]() 上是以
上是以![]() 为上界的有界函数,求实数
为上界的有界函数,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com