
科目: 来源: 题型:
【题目】若A1,A2,…,Am为集合A={1,2,…,n}(n≥2且n∈N*)的子集,且满足两个条件:
①A1∪A2∪…∪Am=A;
②对任意的{x,y}A,至少存在一个i∈{1,2,3,…,m},使Ai∩{x,y}={x}或{y}.则称集合组A1,A2,…,Am具有性质P.
如图,作n行m列数表,定义数表中的第k行第l列的数为akl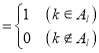 .
.
a11 | a12 | … | a1m |
a21 | a22 | … | a2m |
… | … | … | … |
an1 | an2 | … | anm |
(1)当n=4时,判断下列两个集合组是否具有性质P,如果是请画出所对应的表格,如果不是请说明理由;
集合组1:A1={1,3},A2={2,3},A3={4};
集合组2:A1={2,3,4},A2={2,3},A3={1,4}.
(2)当n=7时,若集合组A1,A2,A3具有性质P,请先画出所对应的7行3列的一个数表,再依此表格分别写出集合A1,A2,A3;
(3)当n=100时,集合组A1,A2,…,At是具有性质P且所含集合个数最小的集合组,求t的值及|A1|+|A2|+…|At|的最小值.(其中|Ai|表示集合Ai所含元素的个数)
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() .
.
(1)若曲线![]() 在点
在点![]() 处的切线与直线
处的切线与直线![]() 垂直,求函数
垂直,求函数![]() 的单调区间;
的单调区间;
(2)若对于任意![]() 都有
都有![]() 成立,试求
成立,试求![]() 的取值范围;
的取值范围;
(3)记![]() .当
.当![]() 时,函数
时,函数![]() 在区间
在区间![]() 上有两个零点,求实数
上有两个零点,求实数![]() 的取值范围。
的取值范围。
查看答案和解析>>
科目: 来源: 题型:
【题目】一个国际象棋棋盘(由8×8个方格组成),其中有一个小方格因破损而被剪去(破损位置不确定).“L”形骨牌由三个相邻的小方格组成,如图所示.现要将这个破损的棋盘剪成数个“L”形骨牌,则( )
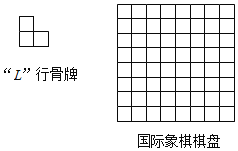
A.至多能剪成19块“L”形骨牌
B.至多能剪成20块“L”形骨牌
C.最多能剪成21块“L”形骨牌
D.前三个答案都不对
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)的图象向左平移1个单位后关于y轴对称,当x2>x1>1时,[f(x2)﹣f(x1)](x2﹣x1)<0恒成立,设a=f(![]() ),b=f(2),c=f(3),则a、b、c的大小关系为( )
),b=f(2),c=f(3),则a、b、c的大小关系为( )
A.c>a>bB.c>b>aC.a>c>bD.b>a>c
查看答案和解析>>
科目: 来源: 题型:
【题目】设![]() 是各项均为非零实数的数列
是各项均为非零实数的数列![]() 的前n项和,给出如下两个命题上:命题p:
的前n项和,给出如下两个命题上:命题p:![]() 是等差数列;命题q:等式
是等差数列;命题q:等式![]() 对任意
对任意![]()
![]() 恒成立,其中k,b是常数.
恒成立,其中k,b是常数.
(1)若p是q的充分条件,求k,b的值;
(2)对于(1)中的k与b,问p是否为q的必要条件,请说明理由;
(3)若p为真命题,对于给定的正整数n![]() 和正数M,数列
和正数M,数列![]() 满足条件
满足条件![]() ,试求
,试求![]() 的最大值.
的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】![]() 的内切圆与三边
的内切圆与三边![]() 的切点分别为
的切点分别为![]() ,已知
,已知![]() ,内切圆圆心
,内切圆圆心![]() ,设点A的轨迹为R.
,设点A的轨迹为R.
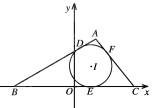
(1)求R的方程;
(2)过点C的动直线m交曲线R于不同的两点M,N,问在x轴上是否存在一定点Q(Q不与C重合),使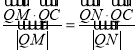 恒成立,若求出Q点的坐标,若不存在,说明理由.
恒成立,若求出Q点的坐标,若不存在,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在四棱柱![]() 中,侧棱
中,侧棱![]() 底面
底面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,(
,(![]() )
)
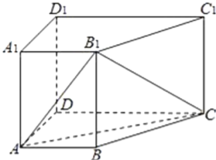
(1)求证:![]() 平面
平面![]() ;
;
(2)若直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,求
,求![]() 的值;
的值;
(3)现将与四棱柱![]() 形状和大小完全相同的两个四棱柱拼成一个新的四棱柱,规定:若拼成的新四棱柱形状和大小完全相同,则视为同一种拼接方案,问共有几种不同的拼接方案?在这些拼接成的新四棱柱中,记其中最小的表面积为
形状和大小完全相同的两个四棱柱拼成一个新的四棱柱,规定:若拼成的新四棱柱形状和大小完全相同,则视为同一种拼接方案,问共有几种不同的拼接方案?在这些拼接成的新四棱柱中,记其中最小的表面积为![]() ,写出
,写出![]() 的解析式.(直接写出答案,不必说明理由)
的解析式.(直接写出答案,不必说明理由)
查看答案和解析>>
科目: 来源: 题型:
【题目】若![]() 是一个集合,
是一个集合,![]() 是一个以
是一个以![]() 的某些子集为元素的集合,且满足:(1)
的某些子集为元素的集合,且满足:(1)![]() 属于
属于![]() ,
,![]() 属于
属于![]() ;(2)
;(2)![]() 中任意多个元素的并集属于
中任意多个元素的并集属于![]() ;(3)
;(3)![]() 中任意多个元素的交集属于
中任意多个元素的交集属于![]() ,则称
,则称![]() 是集合
是集合![]() 上的一个拓补.已知集合
上的一个拓补.已知集合![]() ,对于下面给出的四个集合
,对于下面给出的四个集合![]() :
:
①![]() ②
②![]()
③![]() ④
④![]()
其中是集合![]() 上的拓补的集合
上的拓补的集合![]() 的序号是______.(写出所有的拓补的集合
的序号是______.(写出所有的拓补的集合![]() 的序号)
的序号)
查看答案和解析>>
科目: 来源: 题型:
【题目】设直线系![]() (
(![]() ),则下列命题中是真命题的个数是( )
),则下列命题中是真命题的个数是( )
①存在一个圆与所有直线相交;
②存在一个圆与所有直线不相交;
③存在一个圆与所有直线相切;
④![]() 中所有直线均经过一个定点;
中所有直线均经过一个定点;
⑤不存在定点![]() 不在
不在![]() 中的任一条直线上;
中的任一条直线上;
⑥对于任意整数![]() ,存在正
,存在正![]() 边形,其所有边均在
边形,其所有边均在![]() 中的直线上;
中的直线上;
⑦![]() 中的直线所能围成的正三角形面积都相等.
中的直线所能围成的正三角形面积都相等.
A.3B.4C.5D.6
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,焦距为
,焦距为![]() ,斜率为k的直线l与椭圆M有两个不同的交点A、B.
,斜率为k的直线l与椭圆M有两个不同的交点A、B.
(1)求椭圆M的方程;
(2)设P(﹣2,0),直线PA与椭圆M的另一个交点为C,直线PB与椭圆M的另一个交点为D,若C、D与点![]() 共线,求斜率k的值.
共线,求斜率k的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com