
科目: 来源: 题型:
【题目】如图,已知三棱柱![]() 中,
中,![]() 底面
底面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.![]() ,
,![]() 分别为棱
分别为棱![]() ,
,![]() 的中点.
的中点.
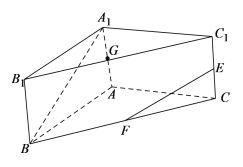
(1)求异面直线![]() 与
与![]() 所成角的大小;
所成角的大小;
(2)若![]() 为线段
为线段![]() 的中点,试在图中作出过
的中点,试在图中作出过![]() 、
、![]() 、
、![]() 三点的平面截该棱柱所得的多边形,并求出以该多边形为底,
三点的平面截该棱柱所得的多边形,并求出以该多边形为底,![]() 为顶点的棱锥的体积.
为顶点的棱锥的体积.
查看答案和解析>>
科目: 来源: 题型:
【题目】在直角坐标系![]() 中,倾斜角为
中,倾斜角为![]() 的直线
的直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).在以坐标原点为极点,
为参数).在以坐标原点为极点,![]() 轴正半轴为极轴的极坐标系中,曲线
轴正半轴为极轴的极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,且
两点,且![]() ,求直线
,求直线![]() 的倾斜角.
的倾斜角.
查看答案和解析>>
科目: 来源: 题型:
【题目】从抛物线![]() 上任意一点P向x轴作垂线段,垂足为Q,点M是线段
上任意一点P向x轴作垂线段,垂足为Q,点M是线段![]() 上的一点,且满足
上的一点,且满足![]()
(1)求点M的轨迹C的方程;
(2)设直线![]() 与轨迹c交于
与轨迹c交于![]() 两点,T为C上异于
两点,T为C上异于![]() 的任意一点,直线
的任意一点,直线![]() ,
,![]() 分别与直线
分别与直线![]() 交于
交于![]() 两点,以
两点,以![]() 为直径的圆是否过x轴上的定点?若过定点,求出符合条件的定点坐标;若不过定点,请说明理由.
为直径的圆是否过x轴上的定点?若过定点,求出符合条件的定点坐标;若不过定点,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】某市房管局为了了解该市市民![]() 年
年![]() 月至
月至![]() 年
年![]() 月期间买二手房情况,首先随机抽样其中
月期间买二手房情况,首先随机抽样其中![]() 名购房者,并对其购房面积
名购房者,并对其购房面积![]() (单位:平方米,
(单位:平方米,![]() )进行了一次调查统计,制成了如图
)进行了一次调查统计,制成了如图![]() 所示的频率分布直方图,接着调查了该市
所示的频率分布直方图,接着调查了该市![]() 年
年![]() 月至
月至![]() 年
年![]() 月期间当月在售二手房均价
月期间当月在售二手房均价![]() (单位:万元/平方米),制成了如图
(单位:万元/平方米),制成了如图![]() 所示的散点图(图中月份代码
所示的散点图(图中月份代码![]() 分别对应
分别对应![]() 年
年![]() 月至
月至![]() 年
年![]() 月).
月).
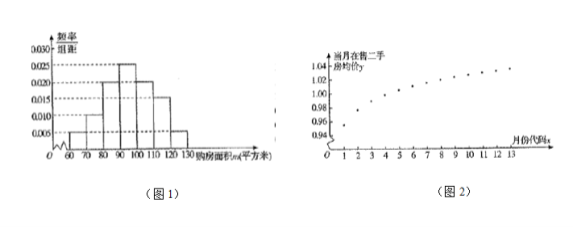
(1)试估计该市市民的购房面积的中位数![]() ;
;
(2)现采用分层抽样的方法从购房面积位于![]() 的
的![]() 位市民中随机抽取
位市民中随机抽取![]() 人,再从这
人,再从这![]() 人中随机抽取
人中随机抽取![]() 人,求这
人,求这![]() 人的购房面积恰好有一人在
人的购房面积恰好有一人在![]() 的概率;
的概率;
(3)根据散点图选择![]() 和
和![]() 两个模型进行拟合,经过数据处理得到两个回归方程,分别为
两个模型进行拟合,经过数据处理得到两个回归方程,分别为![]() 和
和![]() ,并得到一些统计量的值如下表所示:
,并得到一些统计量的值如下表所示:
|
| |
| 0.000591 | 0.000164 |
| 0.006050 | |
请利用相关指数![]() 判断哪个模型的拟合效果更好,并用拟合效果更好的模型预测出
判断哪个模型的拟合效果更好,并用拟合效果更好的模型预测出![]() 年
年![]() 月份的二手房购房均价(精确到
月份的二手房购房均价(精确到![]() )
)
(参考数据)![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
(参考公式)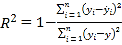
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的离心率
的离心率![]() ,且圆
,且圆![]() 过椭圆
过椭圆![]() 的上,下顶点.
的上,下顶点.
(1)求椭圆![]() 的方程.
的方程.
(2)若直线![]() 的斜率为
的斜率为![]() ,且直线
,且直线![]() 交椭圆
交椭圆![]() 于
于![]() 、
、![]() 两点,点
两点,点![]() 关于点的对称点为
关于点的对称点为![]() ,点
,点![]() 是椭圆
是椭圆![]() 上一点,判断直线
上一点,判断直线![]() 与
与![]() 的斜率之和是否为定值,如果是,请求出此定值:如果不是,请说明理.
的斜率之和是否为定值,如果是,请求出此定值:如果不是,请说明理.
查看答案和解析>>
科目: 来源: 题型:
【题目】某气象站统计了4月份甲、乙两地的天气温度(单位![]() ),统计数据的茎叶图如图所示,
),统计数据的茎叶图如图所示,
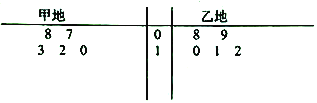
(1)根据所给茎叶图利用平均值和方差的知识分析甲,乙两地气温的稳定性;
(2)气象主管部门要从甲、乙两地各随机抽取一天的天气温度,若甲、乙两地的温度之和大于或等于![]() ,则被称为“甲、乙两地往来温度适宜天气”,求“甲、乙两地往来温度适宜天气”的概率.
,则被称为“甲、乙两地往来温度适宜天气”,求“甲、乙两地往来温度适宜天气”的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】
某营养师要为某个儿童预定午餐和晚餐.已知一个单位的午餐含12个单位的碳水化合物,6个单位的蛋白质和6个单位的维生素![]() ;一个单位的晚餐含8个单位的碳水化合物,6个单位的蛋白质和10个单位的维生素
;一个单位的晚餐含8个单位的碳水化合物,6个单位的蛋白质和10个单位的维生素![]() .另外,该儿童这两餐需要的营养中至少含64个单位的碳水化合物,42个单位的蛋白质和54个单位的维生素
.另外,该儿童这两餐需要的营养中至少含64个单位的碳水化合物,42个单位的蛋白质和54个单位的维生素![]() .如果一个单位的午餐、晚餐的费用分别是2.5元和4元,那么要满足上述的营养要求,并且花费最少,应当为该儿童分别预订多少个单位的午餐和晚餐?
.如果一个单位的午餐、晚餐的费用分别是2.5元和4元,那么要满足上述的营养要求,并且花费最少,应当为该儿童分别预订多少个单位的午餐和晚餐?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com