【题目】已知函数.

（1）讨论的单调性.

（2）试问是否存在，使得对恒成立？若存在，求的取值范围；若不存在，请说明理由.

【题目】某市为了解本市1万名小学生的普通话水平，在全市范围内进行了普通话测试，测试后对每个小学生的普通话测试成绩进行统计，发现总体（这1万名小学生普通话测试成绩）服从正态分布.

（1）从这1万名小学生中任意抽取1名小学生，求这名小学生的普通话测试成绩在内的概率；

（2）现在从总体中随机抽取12名小学生的普通话测试成绩，对应的数据如下：50，52，56，62，63，68，65，64，72，80，67，90.从这12个数据中随机选取4个，记表示大于总体平均分的个数，求的方差.

参考数据：若，则，，.

【题目】如图，在三棱柱中，侧面为菱形，为的中点，为等腰直角三角形，，，且.

（1）证明：平面.

（2）求与平面所成角的正弦值.

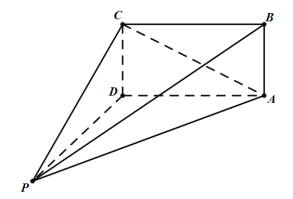
【题目】如图，在四棱锥中，，平面，底面为正方形，且.若四棱锥的每个顶点都在球的球面上，则球的表面积的最小值为_____；当四棱锥的体积取得最大值时，二面角的正切值为_______.

A.20.5B.21元C.21.5元D.22元

（1）若{an}的前n项和Sn＝3n+2，试判断{an}是否是P数列，并说明理由；

（2）设数列a1，a2，a3，…，a10是首项为﹣1、公差为d的等差数列，若该数列是P数列，求d的取值范围；

（3）设无穷数列{an}是首项为a、公比为q的等比数列，有穷数列{bn}，{cn}是从{an}中取出部分项按原来的顺序所组成的不同数列，其所有项和分别为T1，T2，求{an}是P数列时a与q所满足的条件，并证明命题“若a＞0且T1＝T2，则{an}不是P数列”.

【题目】已知椭圆C的中心在坐标原点焦点在x轴上，椭圆C上一点A（2，﹣1）到两焦点距离之和为8.若点B是椭圆C的上顶点，点P，Q是椭圆C上异于点B的任意两点.

（1）求椭圆C的方程；

（2）若BP⊥BQ，且满足32的点D在y轴上，求直线BP的方程；

（3）若直线BP与BQ的斜率乘积为常数λ（λ＜0），试判断直线PQ是否经过定点.若经过定点，请求出定点坐标；若不经过定点，请说明理由.

（1）求药峰浓度与药峰时间（精确到0.01小时），并指出血药浓度随时间的变化趋势；

（2）求血药浓度的半衰期（血药浓度从药峰浓度降到其一半所需要的时间）（精确到0.01小时）.

（1）若3，求△ABC的面积；

（2）若∠B＜∠C，求2cos2B+cos2C的取值范围.

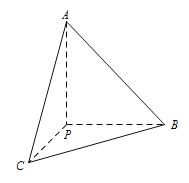
（1）求点A到直线BC的距离；

（2）若D是棱BC的中点，求异面直线PB，AD所成角的大小（结果用反三角函数值表示）.