
科目: 来源: 题型:
【题目】阅读:
已知![]() 、
、![]() ,
,![]() ,求
,求![]() 的最小值.
的最小值.
解法如下:![]() ,
,
当且仅当![]() ,即
,即![]() 时取到等号,
时取到等号,
则![]() 的最小值为
的最小值为![]() .
.
应用上述解法,求解下列问题:
(1)已知![]() ,
,![]() ,求
,求![]() 的最小值;
的最小值;
(2)已知![]() ,求函数
,求函数![]() 的最小值;
的最小值;
(3)已知正数![]() 、
、![]() 、
、![]() ,
,![]() ,
,
求证:![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() ,长轴长为4,
,长轴长为4,![]() ,
,![]() 分别为椭圆
分别为椭圆![]() 的左,右焦点,点
的左,右焦点,点![]() 是椭圆
是椭圆![]() 上的任意一点,
上的任意一点,![]() 面积的最大为
面积的最大为![]() ,且取得最大值时
,且取得最大值时![]() 为钝角.
为钝角.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)已知圆![]() ,点
,点![]() 为圆
为圆![]() 上任意一点,过点
上任意一点,过点![]() 的切线分别交椭圆
的切线分别交椭圆![]() 于
于![]() 两点,且
两点,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某公司生产一种新产品,从产品中抽取100件作为样本,测量这些产品的质量指标值,由测量结果得到如图所示的频率分布直方图.
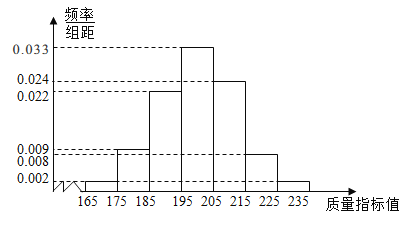
(1)用每组区间的中点值代表该组数据,估算这批产品的样本平均数![]() 和样本方差的
和样本方差的![]() ;
;
(2)从指标值落在![]() 的产品中随机抽取2件做进一步检测,设抽取的产品的指标在
的产品中随机抽取2件做进一步检测,设抽取的产品的指标在![]() 的件数为
的件数为![]() ,求
,求![]() 的分布列和数学期望;
的分布列和数学期望;
(3)由频率分布直方图可以认为,这种产品的质量指标值服从正态分布![]() ,
,![]() 近似为样本平均值
近似为样本平均值![]() ,
,![]() 近似为样本方差
近似为样本方差![]() ,若产品质量指标值大于236.6,则产品不合格,该厂生产10万件该产品,求这批产品不合格的件数.
,若产品质量指标值大于236.6,则产品不合格,该厂生产10万件该产品,求这批产品不合格的件数.
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】四棱锥![]() 的底面是正方形,
的底面是正方形,![]() 平面
平面![]() ,且
,且![]() ,该四棱锥的五个顶点都在同一个球面上,
,该四棱锥的五个顶点都在同一个球面上,![]() 分别是棱
分别是棱![]() 的中点,直线
的中点,直线![]() 被球面所截得的线段长为
被球面所截得的线段长为![]() ,则该球的表面积为( )
,则该球的表面积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】我国古代数学著作《孙子算经》中记有如下问题:“今有五等诸侯,其分橘子六十颗,人別加三颗”,问:“五人各得几何?”其意思为:“现在有5个人分60个橘子,他们分得的橘子个数成公差为3的等差数列,问5人各得多少橘子.”根据这个问题,下列说法错误的是( )
A.得到橘子最多的诸侯比最少的多12个
B.得到橘子的个数排名为正数第3和倒数第3的是同一个人
C.得到橘子第三多的人所得的橘子个数是12
D.所得橘子个数为倒数前3的诸侯所得的橘子总数为24
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系中,曲线![]() 的方程为
的方程为![]() ,以
,以![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 是圆心在极轴上且经过极点的圆,射线
是圆心在极轴上且经过极点的圆,射线![]() 与曲线
与曲线![]() 交于点
交于点![]() .
.
(1)求曲线![]() 的参数方程,
的参数方程,![]() 的极坐标方程;
的极坐标方程;
(2)若![]() ,
,![]() 是曲线
是曲线![]() 上的两点,求
上的两点,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知抛物线![]() ,且过抛物线焦点
,且过抛物线焦点![]() 作直线交抛物线所得最短弦长为
作直线交抛物线所得最短弦长为![]() ,过点
,过点![]() 作斜率存在的动直线
作斜率存在的动直线![]() 与抛物线
与抛物线![]() 交于
交于![]() 两点.
两点.
(1)求抛物线![]() 的方程;
的方程;
(2)若过点![]() 作
作![]() 轴的垂线
轴的垂线![]() ,则
,则![]() 轴上是否存在一点
轴上是否存在一点![]() ,使得直线
,使得直线![]() 与直线
与直线![]() 的交点恒在一条直线上?若存在,求该点的坐标及该定直线的方程;若不存在,请说明理由.
的交点恒在一条直线上?若存在,求该点的坐标及该定直线的方程;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com