
【题目】在平面直角坐标系中,曲线![]() 的方程为
的方程为![]() ,以
,以![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 是圆心在极轴上且经过极点的圆,射线
是圆心在极轴上且经过极点的圆,射线![]() 与曲线
与曲线![]() 交于点
交于点![]() .
.
(1)求曲线![]() 的参数方程,
的参数方程,![]() 的极坐标方程;
的极坐标方程;
(2)若![]() ,
,![]() 是曲线
是曲线![]() 上的两点,求
上的两点,求![]() 的值.
的值.
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率
的离心率![]() ,左、右焦点分别为
,左、右焦点分别为![]() 、
、![]() ,抛物线
,抛物线![]() 的焦点
的焦点![]() 恰好是该椭圆的一个顶点.
恰好是该椭圆的一个顶点.
(1)求椭圆![]() 的方程;
的方程;
(2)已知圆![]() 的切线
的切线![]() (直线
(直线![]() 的斜率存在且不为零)与椭圆相交于
的斜率存在且不为零)与椭圆相交于![]() 、
、![]() 两点,那么以
两点,那么以![]() 为直径的圆是否经过定点?如果是,求出定点的坐标;如果不是,请说明理由.
为直径的圆是否经过定点?如果是,求出定点的坐标;如果不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某超市从![]() 年甲、乙两种酸奶的日销售量(单位:箱)的数据中分别随机抽取
年甲、乙两种酸奶的日销售量(单位:箱)的数据中分别随机抽取![]() 个,并按
个,并按![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 分组,得到频率分布直方图如图,假设甲、乙两种酸奶独立销售且日销售量相互独立.
分组,得到频率分布直方图如图,假设甲、乙两种酸奶独立销售且日销售量相互独立.
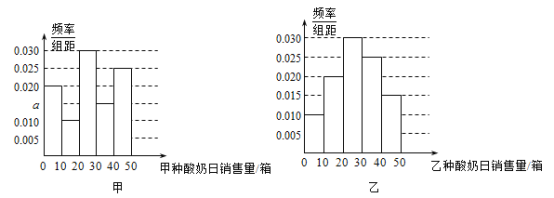
(1)写出频率分布直方图甲中的![]() 的值;记甲种酸奶与乙种酸奶日销售量(单位:箱)的方差分别为
的值;记甲种酸奶与乙种酸奶日销售量(单位:箱)的方差分别为![]() 、
、![]() ,试比较
,试比较![]() 与
与![]() 的大小;(只需写出结论)
的大小;(只需写出结论)
(2)估计在未来的某一天里,甲、乙两种酸奶的销售量恰有一个高于![]() 箱且另一个不高于
箱且另一个不高于![]() 箱的概率;
箱的概率;
(3)设![]() 表示在未来
表示在未来![]() 天内甲种酸奶的日销售量不高于
天内甲种酸奶的日销售量不高于![]() 箱的天数,以日留住量落入各组的频率为概率,求
箱的天数,以日留住量落入各组的频率为概率,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ,长轴长为4,
,长轴长为4,![]() ,
,![]() 分别为椭圆
分别为椭圆![]() 的左,右焦点,点
的左,右焦点,点![]() 是椭圆
是椭圆![]() 上的任意一点,
上的任意一点,![]() 面积的最大为
面积的最大为![]() ,且取得最大值时
,且取得最大值时![]() 为钝角.
为钝角.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)已知圆![]() ,点
,点![]() 为圆
为圆![]() 上任意一点,过点
上任意一点,过点![]() 的切线分别交椭圆
的切线分别交椭圆![]() 于
于![]() 两点,且
两点,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,双曲线![]() 的右顶点为A,右焦点为F,点B在双曲线的右支上,矩形OFBD与矩形AEGF相似,且矩形OFBD与矩形AEGF的面积之比为2:1,则该双曲线的离心率为
的右顶点为A,右焦点为F,点B在双曲线的右支上,矩形OFBD与矩形AEGF相似,且矩形OFBD与矩形AEGF的面积之比为2:1,则该双曲线的离心率为

A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xoy中,以坐标原点O为极点,x轴正半轴为极轴建立极坐标系。已知曲线C的极坐标方程为![]() ,过点
,过点![]() 的直线l的参数方程为
的直线l的参数方程为 (为参数),直线l与曲线C交于M、N两点。
(为参数),直线l与曲线C交于M、N两点。
(1)写出直线l的普通方程和曲线C的直角坐标方程:
(2)若![]() 成等比数列,求a的值。
成等比数列,求a的值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,昆明加大了特色农业建设,其中花卉产业是重要组成部分.昆明斗南毗邻滇池东岸,是著名的花都,有“全国10支鲜花7支产自斗南”之说,享有“金斗南”的美誉.为进一步了解鲜花品种的销售情况,现随机抽取甲、乙两户斗南花农,对其连续5日的玫瑰花日销售情况进行跟踪调查,将日销售量作为样本绘制成茎叶图如下,单位:扎(20支/扎).
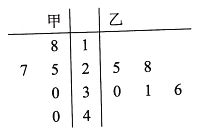
(1)求甲、乙两户花农连续5日的日均销售量,并比较两户花农连续5日销售量的稳定性;
(2)从两户花农连续5日的销售量中各随机抽取一个,求甲的销售量比乙的销售量高的概率·
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com