
科目: 来源: 题型:
【题目】某校高三年级有1000人,某次考试不同成绩段的人数![]() ,且所有得分都是整数.
,且所有得分都是整数.
(1)求全班平均成绩;
(2)计算得分超过141的人数;(精确到整数)
(3)甲同学每次考试进入年级前100名的概率是![]() ,若本学期有4次考试,
,若本学期有4次考试, ![]() 表示进入前100名的次数,写出
表示进入前100名的次数,写出![]() 的分布列,并求期望与方差.
的分布列,并求期望与方差.
参考数据: ![]()
![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】故宫博物院五一期间同时举办“戏曲文化展”、“明代御窖瓷器展”、“历代青绿山水画展”、 “赵孟頫书画展”四个展览.某同学决定在五一当天的上、下午各参观其中的一个,且至少参观一个画展,则不同的参观方案共有
A. 6种 B. 8种 C. 10种 D. 12种
查看答案和解析>>
科目: 来源: 题型:
【题目】对某校高三年级100名学生的视力情况进行统计(如果两眼视力不同,取较低者统计),得到如图所示的频率分布直方图,已知从这100人中随机抽取1人,其视力在![]() 的概率为
的概率为![]() .
.
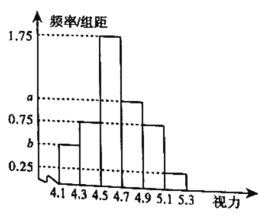
(1)求a,b的值;
(2)若报考高校A专业的资格为:任何一眼裸眼视力不低于5.0,已知在![]() 中有
中有![]() 的学生裸眼视力不低于5.0.现用分层抽样的方法从
的学生裸眼视力不低于5.0.现用分层抽样的方法从![]() 和
和![]() 中抽取4名同学,设这4人中有资格(仅考虑视力)考A专业的人数为随机变量ξ,求ξ的分布列及数学期望.
中抽取4名同学,设这4人中有资格(仅考虑视力)考A专业的人数为随机变量ξ,求ξ的分布列及数学期望.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在三棱锥P-ABC中,![]() ,
,![]() ,
,![]() 平面PAB,D,E分别是AC,BC上的点,且
平面PAB,D,E分别是AC,BC上的点,且![]() 平面PAB.
平面PAB.
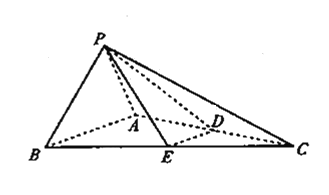
(1)求证![]() 平面PDE;
平面PDE;
(2)若D为线段AC中点,求直线PC与平面PDE所成角的正弦值.
查看答案和解析>>
科目: 来源: 题型:
【题目】在直角坐标系xOy中,曲线C1:![]() ,以O为极点,x轴正半轴为极轴建立极坐标系,曲线C2是圆心极坐标为(3,π),半径为1的圆.
,以O为极点,x轴正半轴为极轴建立极坐标系,曲线C2是圆心极坐标为(3,π),半径为1的圆.
(1)求曲线C1的参数方程和C2的直角坐标方程;
(2)设M,N分别为曲线C1,C2上的动点,求|MN|的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系xOy中,点A(0,﹣3),点M满足|MA|=2|MO|.
(1)求点M的轨迹方程;
(2)若圆C:(x﹣c)2+(y﹣c+1)2=1,判断圆C上是否存在符合题意的M;
(3)设P(x1,y1),Q(x2,y2)是点M轨迹上的两个动点,点P关于点(0,1)的对称点为P1,点P关于直线y=1的对称点为P2,如果直线QP1,QP2与y轴分别交于(0,a)和(0,b),问(a﹣1)(b﹣1)是否为定值?若是,求出该定值;若不是,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
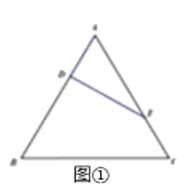
【题目】(题文)
等边△ABC的边长为3,点D,E分别为AB,AC上的点,且满足![]() (如图①),将△ADE沿DE折起到△A1DE的位置,使二面角A1﹣DE﹣B成直二面角,连接A1B,A1C(如图②).
(如图①),将△ADE沿DE折起到△A1DE的位置,使二面角A1﹣DE﹣B成直二面角,连接A1B,A1C(如图②).
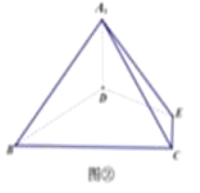
(1)求证:A1D⊥平面BCED;
(2)在线段BC上是否存在点P(不包括端点),使直线PA1与平面A1BD所成的角为60°?若存在,求出A1P的长,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com