
科目: 来源: 题型:
【题目】如图,关于正方体![]() ,有下列四个命题:
,有下列四个命题:
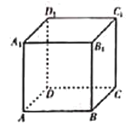
①![]() 与平面
与平面![]() 所成角为45°;
所成角为45°;
②三棱锥![]() 与三棱锥
与三棱锥![]() 的体积比为
的体积比为![]() ;
;
③存在唯一平面![]() .使
.使![]() 平面
平面![]() 且
且![]() 截此正方体所得截面为正六边形;
截此正方体所得截面为正六边形;
④过![]() 作平面
作平面![]() ,使得棱
,使得棱![]() 、
、![]() ,
,![]() 在平面
在平面![]() 上的正投影的长度相等.则这样的平面
上的正投影的长度相等.则这样的平面![]() 有且仅有一个.
有且仅有一个.
上述四个命题中,正确命题的序号为________.
查看答案和解析>>
科目: 来源: 题型:
【题目】造纸术是我国古代四大发明之一,纸张的规格是指纸张制成后,经过修整切边,裁成一定的尺寸.现在我国采用国际标准,规定以![]() 、
、![]() 、…、
、…、![]() ;
;![]() 、
、![]() 、…、
、…、![]() 等标记来表示纸张的幅面规格.复印纸幅面规格只采用
等标记来表示纸张的幅面规格.复印纸幅面规格只采用![]() 系列和
系列和![]() 系列,共中
系列,共中![]() 系列的幅面规格为:①
系列的幅面规格为:①![]() 规格的纸张的幅宽(以
规格的纸张的幅宽(以![]() 表示)和长度(以
表示)和长度(以![]() 表示)的比例关系为
表示)的比例关系为![]() ;②将
;②将![]() 纸张沿长度方向对开成两等分,便成为
纸张沿长度方向对开成两等分,便成为![]() 规格,
规格,![]() 纸张沿长度方向对开成两等分,便成为
纸张沿长度方向对开成两等分,便成为![]() 规格,…,如此对开至
规格,…,如此对开至![]() 规格.现有
规格.现有![]() 、
、![]() 、
、![]() 、…、
、…、![]() 纸各一张.若
纸各一张.若![]() 纸的面积为
纸的面积为![]() .则这9张纸的面积之和等于__________
.则这9张纸的面积之和等于__________![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】天文学中为了衡量星星的明暗程度,古希腊天文学家喜帕恰斯(![]() ,又名依巴谷)在公元前二世纪首先提出了星等这个概念.星等的数值越小,星星就越亮;星等的数值越大,它的光就越暗.到了1850年,由于光度计在天体光度测量中的应用,英国天文学家普森(
,又名依巴谷)在公元前二世纪首先提出了星等这个概念.星等的数值越小,星星就越亮;星等的数值越大,它的光就越暗.到了1850年,由于光度计在天体光度测量中的应用,英国天文学家普森(![]() )又提出了衡量天体明暗程度的亮度的概念.天体的明暗程度可以用星等或亮度来描述.两颗星的星等与亮度满足
)又提出了衡量天体明暗程度的亮度的概念.天体的明暗程度可以用星等或亮度来描述.两颗星的星等与亮度满足![]() .其中星等为
.其中星等为![]() 的星的亮度为
的星的亮度为![]() .已知“心宿二”的星等是1.00.“天津四” 的星等是1.25.“心宿二”的亮度是“天津四”的
.已知“心宿二”的星等是1.00.“天津四” 的星等是1.25.“心宿二”的亮度是“天津四”的![]() 倍,则与
倍,则与![]() 最接近的是(当
最接近的是(当![]() 较小时,
较小时, ![]() )
)
A.1.24B.1.25C.1.26D.1.27
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系![]() 中,过点
中,过点![]() 的动圆恒与
的动圆恒与![]() 轴相切,
轴相切,![]() 为该圆的直径,设点
为该圆的直径,设点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)过点![]() 的任意直线
的任意直线![]() 与曲线
与曲线![]() 交于点
交于点![]() ,
,![]() 为
为![]() 的中点,过点
的中点,过点![]() 作
作![]() 轴的平行线交曲线
轴的平行线交曲线![]() 于点
于点![]() ,
,![]() 关于点
关于点![]() 的对称点为
的对称点为![]() ,除
,除![]() 以外,直线
以外,直线![]() 与
与![]() 是否有其它公共点?说明理由.
是否有其它公共点?说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】某公司为了对某种商品进行合理定价,需了解该商品的月销售量![]() (单位:万件)与月销售单价
(单位:万件)与月销售单价![]() (单位:元/件)之间的关系,对近
(单位:元/件)之间的关系,对近![]() 个月的月销售量
个月的月销售量![]() 和月销售单价
和月销售单价![]()
![]() 数据进行了统计分析,得到一组检测数据如表所示:
数据进行了统计分析,得到一组检测数据如表所示:
月销售单价 |
|
|
|
|
|
|
月销售量 |
|
|
|
|
|
|
(1)若用线性回归模型拟合![]() 与
与![]() 之间的关系,现有甲、乙、丙三位实习员工求得回归直线方程分别为:
之间的关系,现有甲、乙、丙三位实习员工求得回归直线方程分别为:![]() ,
,![]() 和
和![]() ,其中有且仅有一位实习员工的计算结果是正确的.请结合统计学的相关知识,判断哪位实习员工的计算结果是正确的,并说明理由;
,其中有且仅有一位实习员工的计算结果是正确的.请结合统计学的相关知识,判断哪位实习员工的计算结果是正确的,并说明理由;
(2)若用![]() 模型拟合
模型拟合![]() 与
与![]() 之间的关系,可得回归方程为
之间的关系,可得回归方程为![]() ,经计算该模型和(1)中正确的线性回归模型的相关指数
,经计算该模型和(1)中正确的线性回归模型的相关指数![]() 分别为
分别为![]() 和
和![]() ,请用
,请用![]() 说明哪个回归模型的拟合效果更好;
说明哪个回归模型的拟合效果更好;
(3)已知该商品的月销售额为![]() (单位:万元),利用(2)中的结果回答问题:当月销售单价为何值时,商品的月销售额预报值最大?(精确到
(单位:万元),利用(2)中的结果回答问题:当月销售单价为何值时,商品的月销售额预报值最大?(精确到![]() )
)
参考数据:![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为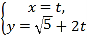 (
(![]() 为参数),以原点
为参数),以原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)写出直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)已知点![]() ,直线
,直线![]() 与曲线
与曲线![]() 相交于点
相交于点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】为提高产品质量,某企业质量管理部门经常不定期地抽查产品进行检测,现在某条生产线上随机抽取100个产品进行相关数据的对比,并对每个产品进行综合评分(满分100分),将每个产品所得的综合评分制成如图所示的频率分布直方图.记综合评分为80分及以上的产品为一等品.
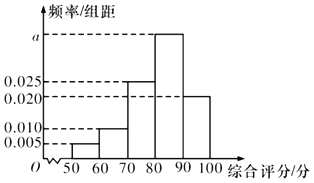
(1)求图中![]() 的值,并求综合评分的中位数;
的值,并求综合评分的中位数;
(2)用样本估计总体,以频率作为概率,按分层抽样的思想,先在该条生产线中随机抽取5个产品,再从这5个产品中随机抽取2个产品记录有关数据,求这2个产品中恰有一个一等品的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).在以坐标原点为极点,
为参数).在以坐标原点为极点,![]() 轴正半轴为极轴的极坐标系中,曲线
轴正半轴为极轴的极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出![]() 的普通方程和
的普通方程和![]() 的直角坐标方程;
的直角坐标方程;
(2)若![]() 与
与![]() 相交于
相交于![]()
![]() 两点,求
两点,求![]() 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com