
科目: 来源: 题型:
【题目】已知曲线C的参数方程为![]() (
(![]() 为参数),P是曲线C上的点且对应的参数为
为参数),P是曲线C上的点且对应的参数为![]() ,
,![]() .直线l过点P且倾斜角为
.直线l过点P且倾斜角为![]() .
.
(1)求曲线C的普通方程和直线l的参数方程.
(2)已知直线l与x轴,y轴分别交于![]() ,求证:
,求证:![]() 为定值.
为定值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆与双曲线![]() 有相同的焦点坐标,且点
有相同的焦点坐标,且点![]() 在椭圆上.
在椭圆上.
(1)求椭圆的标准方程;
(2)设A、B分别是椭圆的左、右顶点,动点M满足![]() ,垂足为B,连接AM交椭圆于点P(异于A),则是否存在定点T,使得以线段MP为直径的圆恒过直线BP与MT的交点Q,若存在,求出点T的坐标;若不存在,请说明理由.
,垂足为B,连接AM交椭圆于点P(异于A),则是否存在定点T,使得以线段MP为直径的圆恒过直线BP与MT的交点Q,若存在,求出点T的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】在如图所示的六面体中,四边形ABCD是边长为2的正方形,四边形ABEF是梯形,![]() ,平面
,平面![]() 平面ABEF,BE=2AF=2,EF
平面ABEF,BE=2AF=2,EF![]() .
.
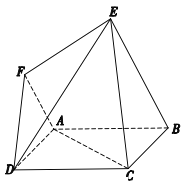
(1)在图中作出平面ABCD与平面DEF的交线,并写出作图步骤,但不要求证明;
(2)求证:![]() 平面DEF;
平面DEF;
(3)求平面ABEF与平面ECD所成锐二面角的余弦值.
查看答案和解析>>
科目: 来源: 题型:
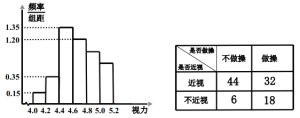
【题目】眼保健操是一种眼睛的保健体操,主要是通过按摩眼部穴位,调整眼及头部的血液循环,调节肌肉,改善眼的疲劳,达到预防近视等眼部疾病的目的.某学校为了调查推广眼保健操对改善学生视力的效果,在应届高三的全体800名学生中随机抽取了100名学生进行视力检查,并得到如图的频率分布直方图.
(1)若直方图中后三组的频数成等差数列,试估计全年级视力在5.0以上的人数;
(2)为了研究学生的视力与眼保健操是否有关系,对年级不做眼保健操和坚持做眼保健操的学生进行了调查,得到下表中数据,根据表中的数据,能否在犯错的概率不超过0.005的前提下认为视力与眼保健操有关系?
(3)在(2)中调查的100名学生中,按照分层抽样在不近视的学生中抽取8人,进一步调查他们良好的护眼习惯,在这8人中任取2人,记坚持做眼保健操的学生人数为X,求X的分布列和数学期望.
附: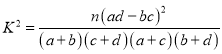
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
k | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
科目: 来源: 题型:
【题目】下图是某省从1月21日至2月24日的新冠肺炎每日新增确诊病例变化曲线图.

若该省从1月21日至2月24日的新冠肺炎每日新增确诊人数按日期顺序排列构成数列![]() ,
,![]() 的前n项和为
的前n项和为![]() ,则下列说法中正确的是( )
,则下列说法中正确的是( )
A.数列![]() 是递增数列B.数列
是递增数列B.数列![]() 是递增数列
是递增数列
C.数列![]() 的最大项是
的最大项是![]() D.数列
D.数列![]() 的最大项是
的最大项是![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面坐标系中xOy中,已知直线l的参数方程为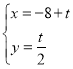 (t为参数),曲线C的参数方程为
(t为参数),曲线C的参数方程为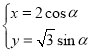 (
(![]() 为参数).以O为极点,x轴的非负半轴为极轴,建立极坐标系.
为参数).以O为极点,x轴的非负半轴为极轴,建立极坐标系.
(1)求曲线C的普通方程和直线l的极坐标方程;
(2)设P为曲线C上的动点,求点P到直线l的距离的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的上顶点为
的上顶点为![]() ,右焦点为F,连结TF并延长与椭圆
,右焦点为F,连结TF并延长与椭圆![]() 交于点S,且
交于点S,且![]() .
.

(1)求椭圆![]() 的方程;
的方程;
(2)已知直线![]() 与x轴交于点M,过点M的直线AB与
与x轴交于点M,过点M的直线AB与![]() 交于A、B两点,点P为直线
交于A、B两点,点P为直线![]() 上任意一点,设直线AB与直线
上任意一点,设直线AB与直线![]() 交于点N,记PA,PB,PN的斜率分别为
交于点N,记PA,PB,PN的斜率分别为![]() ,
,![]() ,
,![]() ,则是否存在实数
,则是否存在实数![]() ,使得
,使得![]() 恒成立?若是,请求出
恒成立?若是,请求出![]() 的值;若不是,请说明理由.
的值;若不是,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示1,已知四边形ABCD满足![]() ,
,![]() ,E是BC的中点.将
,E是BC的中点.将![]() 沿着AE翻折成
沿着AE翻折成![]() ,使平面
,使平面![]() 平面AECD,F为CD的中点,如图所示2.
平面AECD,F为CD的中点,如图所示2.
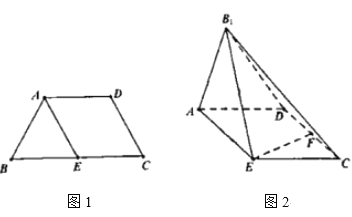
(1)求证:![]() 平面
平面![]() ;
;
(2)求AE到平面![]() 的距离.
的距离.
查看答案和解析>>
科目: 来源: 题型:
【题目】某某大学艺术专业400名学生参加某次测评,根据男女学生人数比例,使用分层抽样的方法从中随机抽取了100名学生,记录他们的分数,将数据分成7组: ![]() ,并整理得到如下频率分布直方图:
,并整理得到如下频率分布直方图:
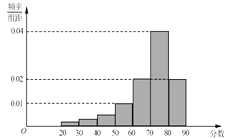
(Ⅰ)从总体的400名学生中随机抽取一人,估计其分数小于70的概率;
(Ⅱ)已知样本中分数小于40的学生有5人,试估计总体中分数在区间[40,50)内的人数;
(Ⅲ)已知样本中有一半男生的分数不小于70,且样本中分数不小于70的男女生人数相等.试估计总体中男生和女生人数的比例.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com