A.“”是“”的充分不必要条件

B.命题“若，则”的逆否命题为：“若，则”

C.若为假命题，则，均为假命题

D.命题，使得，则，使得

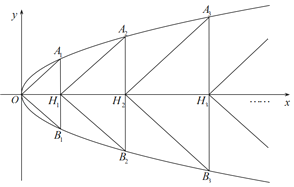
（1）求S1和S2的值;

（2）证明:n≤sn≤n2.

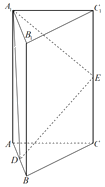
（1）求DE与平面ABC夹角的正弦值;

（2）求二面角A﹣A1D﹣E的余弦值.

（1）若an=2n,且(bn,bn+1)是数列{an}的一个等比拆分,求{bn}的通项公式;

（2）设(bn,cn)是数列{an}的一个等比拆分,且记{bn},{cn}的公比分别为q1,q2;

①若{an}是公比为q的等比数列,求证:q1=q2=q;

②若a1=1,a2=2,q1q2=﹣1,且对任意n∈N*,an+13<anan+1an+2+an+2﹣an恒成立,求a3的取值范围.

【题目】已知函数且a≠1,函数.

（1）判断并证明f(x)和g(x)的奇偶性;

（2）求g(x)的值域;

（3）若x∈R,都有|f(x)|≥|g(x)|成立,求a的取值范围.

【题目】已知椭圆1(a>b>0)的左右焦点分别为F1F2,左右顶点分别为AB,上顶点为T,且△TF1F2为等边三角形.

（1）求此椭圆的离心率e;

（2）若直线y=kx+m(k>0)与椭圆交与CD两点(点D在x轴上方),且与线段F1F2及椭圆短轴分别交于点MN(其中MN不重合),且|CM|=|DN|.

①求k的值;

②设ADBC的斜率分别为k1,k2,求的取值范围.

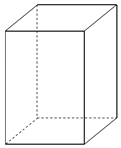
（1）请你确定x的值,使得该容器的外表面积最小;

（2）若该容器全部由某种每平方米价格为100元的材料做成,且制作该容器仅需将购置的材料做成符合需要的矩形,这些矩形即是直四棱柱形容器的上下底面和侧面(假设这一过程中产生的费用和材料损耗可忽略不计),再将这些上下底面和侧面的边缘进行焊接即可做成该容器,焊接费用是每米500元,试确定x的值,使得生产每个该种容器的成本(即原料购置成本+焊接费用)最低.

（1）连结BD,BD1,证明:平面BDD1⊥平面A1BC1;

（2）已知P,Q,R分别是正方形ABCDCDD1C1ADD1A1的中心(即对角线交点),证明:平面PQR∥平面A1BC1.

【题目】如图，在多面体中，四边形为正方形，，，.

（1）证明：平面平面.

（2）若平面，二面角为，三棱锥的外接球的球心为，求二面角的余弦值.