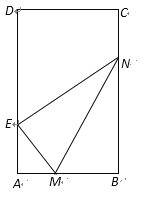
【题目】已知矩形纸片中，，将矩形纸片的右下角沿线段折叠，使矩形的顶点B落在矩形的边上，记该点为E，且折痕的两端点M，N分别在边上.设，的面积为S.

（1）将l表示成θ的函数，并确定θ的取值范围；

（2）求l的最小值及此时的值；

（3）问当θ为何值时，的面积S取得最小值？并求出这个最小值.

【题目】已知函数．

（1）求函数的零点；

（2）设函数的图象与函数的图象交于，两点，求证：；

（3）若，且不等式对一切正实数x恒成立，求k的取值范围．

【题目】设为偶函数，且当时，；当时，．关于函数的零点，有下列三个命题：

①当时，存在实数m，使函数恰有5个不同的零点；

②若，函数的零点不超过4个，则；

③对，，函数恰有4个不同的零点，且这4个零点可以组成等差数列．

其中，正确命题的序号是_______．

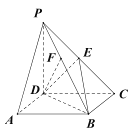
【题目】如图，在四棱锥中，底面是平行四边形，平面，是棱上的一点，满足平面.

（Ⅰ）证明：；

（Ⅱ）设，，若为棱上一点，使得直线与平面所成角的大小为30°，求的值.

（1）估计这100辆汽车的单次最大续航里程的平均值（同一组中的数据用该组区间的中点值代表）.

（2）根据大量的汽车测试数据，可以认为这款汽车的单次最大续航里程近似地服从正态分布，经计算第（1）问中样本标准差的近似值为50。用样本平均数作为的近似值，用样本标准差作为的估计值，现任取一辆汽车，求它的单次最大续航里程恰在250千米到400千米之间的概率.

参考数据：若随机变量服从正态分布，则，，.

（3）某汽车销售公司为推广此款新能源汽车，现面向意向客户推出“玩游戏，送大奖”活动，客户可根据抛掷硬币的结果，操控微型遥控车在方格图上行进，若遥控车最终停在“胜利大本营”，则可获得购车优惠券3万元。已知硬币出现正、反面的概率都是0.5方格图上标有第0格、第1格、第2格、…、第20格。遥控车开始在第0格，客户每掷一次硬币，遥控车向前移动一次。若掷出正面，遥控车向前移动一格（从到）若掷出反面遥控车向前移动两格（从到），直到遥控车移到第19格胜利大本营）或第20格（失败大本营）时，游戏结束。设遥控车移到第格的概率为P试证明是等比数列，并求参与游戏一次的顾客获得优惠券金额的期望值。

【题目】在平面直角坐标系中，直线的参数方程为（为参数），以坐标原点为极点，轴的正半轴为极轴的极坐标系中，曲线的极坐标方程为.

（1）若，求直线以及曲线的直角坐标方程；

（2）若直线与曲线交于两点，且，求直线的斜率.

【题目】已知，分别为双曲线的左、右焦点，以为直径的圆与双曲线在第一象限和第三象限的交点分别为，，设四边形的周长为，面积为，且满足，则该双曲线的离心率为______.

【题目】焦点在x轴上的椭圆C：经过点，椭圆C的离心率为．，是椭圆的左、右焦点，P为椭圆上任意点．

（1）求椭圆的标准方程；

（2）若点M为的中点（O为坐标原点），过M且平行于OP的直线l交椭圆C于A，B两点，是否存在实数，使得；若存在，请求出的值，若不存在，请说明理由．

【题目】将一颗均匀的骰子掷两次，第一次得到的点数记为，第一次得到的点数记为，则方程组有唯一解的概率是___________．

【题目】关于函数有下述四个结论：

①是偶函数；②在区间单调递减；

③在有个零点；④的最大值为.

其中所有正确结论的编号是（ ）

A.①②④B.②④C.①④D.①③