
科目: 来源: 题型:
【题目】十九世纪末,法国学者贝特朗在研究几何概型时提出了“贝特朗悖论”,即“在一个圆内任意选一条弦,这条弦的弦长长于这个圆的内接等边三角形边长的概率是多少?”贝特朗用“随机半径”、“随机端点”、“随机中点”三个合理的求解方法,但结果都不相同.该悖论的矛头直击概率概念本身,强烈地刺激了概率论基础的严格化.已知“随机端点”的方法如下:设A为圆O上一个定点,在圆周上随机取一点B,连接AB,所得弦长AB大于圆O的内接等边三角形边长的概率.则由“随机端点”求法所求得的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】第三届移动互联创新大赛,于2017年3月~10月期间举行,为了选出优秀选手,某高校先在计算机科学系选出一种子选手![]() ,再从全校征集出3位志愿者分别与
,再从全校征集出3位志愿者分别与![]() 进行一场技术对抗赛,根据以往经验,
进行一场技术对抗赛,根据以往经验, ![]() 与这三位志愿者进行比赛一场获胜的概率分别为
与这三位志愿者进行比赛一场获胜的概率分别为![]() ,且各场输赢互不影响.
,且各场输赢互不影响.
(1)求甲恰好获胜两场的概率;
(2)求甲获胜场数的分布列与数学期望.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知数列![]() ,其中
,其中![]() .
.
(1)若![]() 满足
满足![]() .
.
①当![]() ,且
,且![]() 时,求
时,求![]() 的值;
的值;
②若存在互不相等的正整数![]() ,满足
,满足![]() ,且
,且![]() 成等差数列,求
成等差数列,求![]() 的值.
的值.
(2)设数列![]() 的前
的前![]() 项和为
项和为![]() ,数列
,数列![]() 的前n项和为
的前n项和为![]() ,
,![]() ,
,![]() ,若
,若![]() ,
,![]() ,且
,且![]() 恒成立,求
恒成立,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目: 来源: 题型:
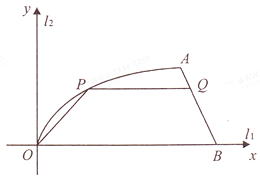
【题目】如图,某小区内有两条互相垂直的道路![]() 与
与![]() ,平面直角坐标系
,平面直角坐标系![]() 的第一象限有一块空地
的第一象限有一块空地![]() ,其边界
,其边界![]() 是函数
是函数![]() 的图象,前一段曲线
的图象,前一段曲线![]() 是函数
是函数![]() 图象的一部分,后一段
图象的一部分,后一段![]() 是一条线段.测得
是一条线段.测得![]() 到
到![]() 的距离为8米,到
的距离为8米,到![]() 的距离为16米,
的距离为16米,![]() 长为20米.
长为20米.
(1)求函数![]() 的解析式;
的解析式;
(2)现要在此地建一个社区活动中心,平面图为梯形![]() (其中
(其中![]() ,
,![]() 为两底边),问:梯形的高为多少米时,该社区活动中心的占地面积最大,并求出最大面积.
为两底边),问:梯形的高为多少米时,该社区活动中心的占地面积最大,并求出最大面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】某人某天的工作是驾车从![]() 地出发,到
地出发,到![]() 两地办事,最后返回
两地办事,最后返回![]() 地,
地,![]() ,三地之间各路段行驶时间及拥堵概率如下表
,三地之间各路段行驶时间及拥堵概率如下表
路段 | 正常行驶所用时间(小时) | 上午拥堵概率 | 下午拥堵概率 |
| 1 | 0.3 | 0.6 |
| 2 | 0.2 | 0.7 |
| 3 | 0.3 | 0.9 |
若在某路段遇到拥堵,则在该路段行驶时间需要延长1小时.
现有如下两个方案:
方案甲:上午从![]() 地出发到
地出发到![]() 地办事然后到达
地办事然后到达![]() 地,下午从
地,下午从![]() 地办事后返回
地办事后返回![]() 地;
地;
方案乙:上午从![]() 地出发到
地出发到![]() 地办事,下午从
地办事,下午从![]() 地出发到达
地出发到达![]() 地,办完事后返回
地,办完事后返回![]() 地.
地.
(1)若此人早上8点从![]() 地出发,在各地办事及午餐的累积时间为2小时,且采用方案甲,求他当日18点或18点之前能返回
地出发,在各地办事及午餐的累积时间为2小时,且采用方案甲,求他当日18点或18点之前能返回![]() 地的概率.
地的概率.
(2)甲乙两个方案中,哪个方案有利于办完事后更早返回![]() 地?请说明理由.
地?请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() 的两个焦点分别为
的两个焦点分别为![]() 点
点![]() 是椭圆上任意一点,且
是椭圆上任意一点,且![]() 的最大值为4,椭圆
的最大值为4,椭圆![]() 的离心率与双曲线
的离心率与双曲线![]() 的离心率互为倒数.
的离心率互为倒数.
(1)求椭圆方程;
(2)设点![]() ,过点
,过点![]() 作直线
作直线![]() 与圆
与圆![]() 相切且分别交椭圆于
相切且分别交椭圆于![]() ,求直线
,求直线![]() 的斜率.
的斜率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com