
科目: 来源: 题型:
【题目】已知直线![]() 与抛物线
与抛物线![]() :
:![]() 交于
交于![]() ,
,![]() 两点,且
两点,且![]() 的面积为16(
的面积为16(![]() 为坐标原点).
为坐标原点).
(1)求![]() 的方程;
的方程;
(2)直线![]() 经过
经过![]() 的焦点
的焦点![]() 且
且![]() 不与
不与![]() 轴垂直,与
轴垂直,与![]() 交于
交于![]() ,
,![]() 两点,若线段
两点,若线段![]() 的垂直平分线与
的垂直平分线与![]() 轴交于点
轴交于点![]() ,证明:
,证明:![]() 为定值.
为定值.
查看答案和解析>>
科目: 来源: 题型:
【题目】国家每年都会对中小学生进行体质健康监测,一分钟跳绳是监测的项目之一.今年某小学对本校六年级300名学生的一分钟跳绳情况做了统计,发现一分钟跳绳个数最低为10,最高为189.现将跳绳个数分成![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 6组,并绘制出如下的频率分布直方图.
6组,并绘制出如下的频率分布直方图.
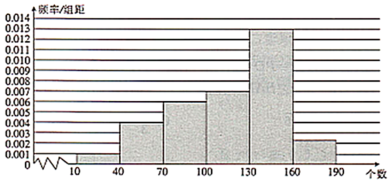
(1)若一分钟跳绳个数达到160为优秀,求该校六年级学生一分钟跳绳为优秀的人数;
(2)上级部门要对该校体质监测情况进行复查,发现每组男、女学生人数比例有很大差别,![]() 组男、女人数之比为
组男、女人数之比为![]() ,
,![]() 组男、女人数之比为
组男、女人数之比为![]() ,
,![]() 组男、女人数之比为
组男、女人数之比为![]() ,
,![]() 组男、女人数之比为
组男、女人数之比为![]() ,
,![]() 组男、女人数之比为
组男、女人数之比为![]() ,
,![]() 组男、女人数之比为
组男、女人数之比为![]() .试估计此校六年级男生一分钟跳绳个数的平均数(同一组中的数据用该组区间的中点值作代表,结果保留整数).
.试估计此校六年级男生一分钟跳绳个数的平均数(同一组中的数据用该组区间的中点值作代表,结果保留整数).
查看答案和解析>>
科目: 来源: 题型:
【题目】2019年庆祝中华人民共和国成立70周年阅兵式彰显了中华民族从站起来、富起来迈向强起来的雄心壮志.阅兵式规模之大、类型之全均创历史之最,编组之新、要素之全彰显强军成就.装备方阵堪称“强军利刃”“强国之盾”,见证着人民军队迈向世界一流军队的坚定步伐.此次大阅兵不仅得到了全中国人的关注,还得到了无数外国人的关注.某单位有6位外国人,其中关注此次大阅兵的有5位,若从这6位外国人中任意选取2位做一次采访,则被采访者都关注了此次大阅兵的概率为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】为解决城市的拥堵问题,某城市准备对现有的一条穿城公路MON进行分流,已知穿城公路MON自西向东到达城市中心点O后转向东北方向(即![]() ).现准备修建一条城市高架道路L,L在MO上设一出入口A,在ON上设一出入口B.假设高架道路L在AB部分为直线段,且要求市中心O与AB的距离为10km.
).现准备修建一条城市高架道路L,L在MO上设一出入口A,在ON上设一出入口B.假设高架道路L在AB部分为直线段,且要求市中心O与AB的距离为10km.
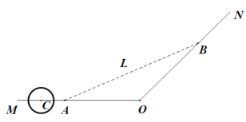
(1)求两站点A,B之间距离的最小值;
(2)公路MO段上距离市中心O30km处有一古建筑群C,为保护古建筑群,设立一个以C为圆心,5km为半径的圆形保护区.则如何在古建筑群C和市中心O之间设计出入口A,才能使高架道路L及其延伸段不经过保护区(不包括临界状态)?
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系中,直线l的参数方程为 为参数),以原点O为极点,x轴的正半轴为极轴建立极坐标系,圆C的极坐标方程为ρ=asinθ(a≠0).
为参数),以原点O为极点,x轴的正半轴为极轴建立极坐标系,圆C的极坐标方程为ρ=asinθ(a≠0).
(1)求圆C的直角坐标方程与直线l的普通方程;
(2)设直线l截圆C的弦长是半径长的![]() 倍,求a的值.
倍,求a的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知动圆![]() 过定点
过定点![]() ,且与定直线
,且与定直线![]() 相切.
相切.
(1)求动圆圆心![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)过点![]() 的任一条直线
的任一条直线![]() 与轨迹
与轨迹![]() 交于不同的两点
交于不同的两点![]() ,试探究在
,试探究在![]() 轴上是否存在定点
轴上是否存在定点![]() (异于点
(异于点![]() ),使得
),使得![]() ?若存在,求点
?若存在,求点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图是某地区2012年至2018年生活垃圾无害化处理量(单位:万吨)的折线图.
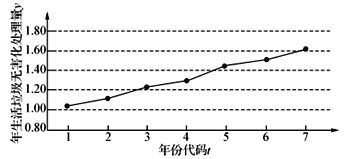
注:年份代码![]() 分别表示对应年份
分别表示对应年份![]() .
.
(1)由折线图看出,可用线性回归模型拟合![]() 与
与![]() 的关系,请用相关系数
的关系,请用相关系数![]() (
(![]() 线性相关较强)加以说明;
线性相关较强)加以说明;
(2)建立![]() 与
与![]() 的回归方程(系数精确到0.01),预测2019年该区生活垃圾无害化处理量.
的回归方程(系数精确到0.01),预测2019年该区生活垃圾无害化处理量.
(参考数据)![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
(参考公式)相关系数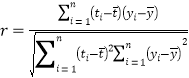 ,在回归方程
,在回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为: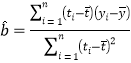 ,
,![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知集合A={1,2,3,4,5,6,7,8,9),在集合A中任取三个元素,分别作为一个三位数的个位数,十位数和百位数,记这个三位数为a,现将组成a的三个数字按从小到大排成的三位数记为I(a),按从大到小排成的三位数记为D(a)(例如a=219,则I(a)=129,D(a)=921),阅读如图所示的程序框图,运行相应的程序,任意输入一个a,则输出b的值为( )
A. 792 B. 693 C. 594 D. 495
查看答案和解析>>
科目: 来源: 题型:
【题目】某中学2018年的高考考生人数是2015年高考考生人数的![]() 倍,为了更好地对比该校考生的升学情况,统计了该校2015年和2018年的高考情况,得到如图柱状图:
倍,为了更好地对比该校考生的升学情况,统计了该校2015年和2018年的高考情况,得到如图柱状图:

则下列结论正确的是![]()
![]()
A. 与2015年相比,2018年一本达线人数减少
B. 与2015年相比,2018年二本达线人数增加了![]() 倍
倍
C. 2015年与2018年艺体达线人数相同
D. 与2015年相比,2018年不上线的人数有所增加
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com