
| A�� | ������ܶ�Ϊ$\frac{3��{G}_{1}}{G{T}^{2}��{G}_{2}-{G}_{1}��}$ | |
| B�� | ������ܶ�Ϊ$\frac{3��{G}_{2}}{G{T}^{2}��{G}_{2}-{G}_{1}��}$ | |
| C�� | ���������ת����Ϊ$\sqrt{\frac{{G}_{2}-{G}_{1}}{{G}_{2}}}$Tʱ�����ڵ����������ϵ����岻�ٶԵ�����ѹ�� | |
| D�� | ���������ת����Ϊ$\sqrt{\frac{{G}_{2}-{G}_{1}}{{G}_{1}}}$Tʱ�����ڵ����������ϵ����岻�ٶԵ�����ѹ�� |
���� �������������������������������������������������������������Ƶ�����ת�����������֮���������������ɹ�ʽ��ʽ��⼴�ɣ�
��� �⣺����������ΪM���뾶ΪR���������������Ϊm��
�ڳ����$G\frac{Mm}{{R}^{2}}={G}_{1}+mR\frac{4{��}^{2}}{{T}^{2}}$
��������${G}_{2}=G\frac{Mm}{{R}^{2}}$
��������Ϊ $V=\frac{4}{3}��{R^3}$
������ܶ�Ϊ $��=\frac{M}{V}$
��ã���=$\frac{3��{G}_{2}}{G{T}^{2}��{G}_{2}-{G}_{1}��}$����A����B��ȷ��
C�������ڵ����������ϵ����岻�ٶԵ�����ѹ��ʱ��${G}_{2}=mR•\frac{4{��}^{2}}{T{��}^{2}}$
���ԣ�T��=$T•\sqrt{\frac{{G}_{2}-{G}_{1}}{{G}_{2}}}$����C��ȷ��D����
��ѡ��BC
���� ����ؼ�����ȷ�����λ��������������������������֮�ͣ�Ȼ���������������ɹ�ʽ��ʽ��⣮


 ��������ܸ�ϰϵ�д�
��������ܸ�ϰϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
 ��ͼ��ʾ��б����̶���ˮƽ�����ϣ�һ��������б��������ƽ��б�����F1�����£���б�������ٶ�Ϊv1�������˶���F1�Ĺ���ΪP1��������������б��б���ϵ�����б��н�Ϊ������F2����ͼ�������£���ͬһб�������ٶ�ҲΪv1�������˶���F2�Ĺ���ΪP2��������˵������ȷ���ǣ�������
��ͼ��ʾ��б����̶���ˮƽ�����ϣ�һ��������б��������ƽ��б�����F1�����£���б�������ٶ�Ϊv1�������˶���F1�Ĺ���ΪP1��������������б��б���ϵ�����б��н�Ϊ������F2����ͼ�������£���ͬһб�������ٶ�ҲΪv1�������˶���F2�Ĺ���ΪP2��������˵������ȷ���ǣ�������| A�� | F2һ������F1 | B�� | F2����С��F1 | C�� | P1һ��С��P2 | D�� | P1һ������P2 |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | ���ٶȲ�Ϊ�� | B�� | ���ٶ�Ϊ1m/s2 | ||
| C�� | ǰ2s�ڵ�ƽ���ٶ���2m/s | D�� | ����1s�ڵ��ٶ���������1m/s |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
 һ���綯�����ڵ���r=2������R=8���ĵ��贮��������Ȧ�ϣ���ͼ��ʾ����֪��Ȧ���Ϊ0.05$\sqrt{2}$m2����100�ѣ���Ȧ�ĵ���Ϊ2������Ȧ��B=$\frac{2}{��}$T����ǿ�ų�����OO1��ת��n=10r/s����ת��ʱ���ں��Ͽ���S��綯����������ʱ����ѹ����ʾ��Ϊ100V��������˵����ȷ���ǣ�������
һ���綯�����ڵ���r=2������R=8���ĵ��贮��������Ȧ�ϣ���ͼ��ʾ����֪��Ȧ���Ϊ0.05$\sqrt{2}$m2����100�ѣ���Ȧ�ĵ���Ϊ2������Ȧ��B=$\frac{2}{��}$T����ǿ�ų�����OO1��ת��n=10r/s����ת��ʱ���ں��Ͽ���S��綯����������ʱ����ѹ����ʾ��Ϊ100V��������˵����ȷ���ǣ�������| A�� | ��Ӧ�綯�Ƶ����ֵΪ100$\sqrt{2}$V | |
| B�� | �綯����������ʱ���������Ϊ800W | |
| C�� | ��ͼʾλ�ÿ�ʼ��ʱ����Ȧ������Ӧ�綯�Ƶı���ʽe1=$\sqrt{2}$sin��20t��V | |
| D�� | ���رպ�ʱ����ͼʾλ�ÿ�ʼ��ʱ����Ȧת��45��ǵĹ��̣�R�ϲ����Ľ�����Ϊ10J |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ʵ����
| ���� | x1 | x2 | x3 | x4 | x5 | x6 |
| ��ֵ����10-2m�� | 0.19 | 0.76 | 1.71 | 3.06 | 4.78 | 6.86 |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ʵ����
 ��1����ͼʵ��װ�ÿ��о�С�����ȱ���ֱ���˶�ʱ�ٶ���ʱ��仯�Ĺ��ɣ�����˵����ȷ����AD
��1����ͼʵ��װ�ÿ��о�С�����ȱ���ֱ���˶�ʱ�ٶ���ʱ��仯�Ĺ��ɣ�����˵����ȷ����AD
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | �������������ܸߵĵ�Ų� | |
| B�� | ��˥���ʵ���Ǻ��ڵ�����ת����һ�����Ӻ�һ������ | |
| C�� | ��������ԭ�ӵ��ڲ���ӷ���ԾǨʱ�ͷŵ� | |
| D�� | �����¡������ߵĵ��뱾��������ǿ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
| A�� | ����̥������ԽѹԽ�����������ڷ��Ӽ���ڳ��� | |
| B�� | Һ�������������������Ƿ��������õı��� | |
| C�� | ������ˮ�л��ۿ����IJ����˶���ӳ�˻����з�������������˶� | |
| D�� | ��ʪ���¶ȼƵ�ʾ����Խ��ʾ������ˮ�����뱥��״̬ԽԶ | |
| E�� | Һ���Ĺ�ѧ������ijЩ�������ƣ����и������� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ʵ����
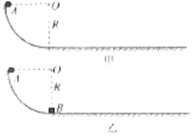 ������ͼ��ʾ�ķ�ʽ��֤��ײ�еĶ����غ㣬��ֱƽ���ڵ��ķ�֮һ�⻬Բ������¶���ˮƽ�������У��Ƚ�С����A��Բ���������ߵ����ٶ��ͷţ�������������ˮƽ���滬�еľ���x1��ͼ�ף���Ȼ��С����B����Բ���������͵㣬�ٽ�A��Բ���������ߵ����ٶ��ͷţ�A��B��ײ����Ϊһ�����壬���������������滬���ľ���x2��ͼ�ң���Բ������İ뾶ΪR��A��B��ȫ��ͬ���������ٶ�Ϊg��
������ͼ��ʾ�ķ�ʽ��֤��ײ�еĶ����غ㣬��ֱƽ���ڵ��ķ�֮һ�⻬Բ������¶���ˮƽ�������У��Ƚ�С����A��Բ���������ߵ����ٶ��ͷţ�������������ˮƽ���滬�еľ���x1��ͼ�ף���Ȼ��С����B����Բ���������͵㣬�ٽ�A��Բ���������ߵ����ٶ��ͷţ�A��B��ײ����Ϊһ�����壬���������������滬���ľ���x2��ͼ�ң���Բ������İ뾶ΪR��A��B��ȫ��ͬ���������ٶ�Ϊg���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com