
分析 (1)根据库仑定律与牛顿第二定律,即可求解加速度大小;由能量守恒定律,结合动能与电势能的表达式,即可求解速度大小;
(2)根据能量守恒定律,结合α粒子减速为零时,两者间距即为金原子核的直径,从而即可求解.
解答 解:(1)由题意可知,距离这个金核r1时,其速度为v1,加速度为a1,根据库仑定律,及牛顿第二定律,则有:a1=$\frac{{F}_{1}}{m}$=$\frac{k\frac{Qq}{{r}_{1}^{2}}}{m}$=$\frac{kQq}{m{r}_{1}^{2}}$;
当距离这个金核r2时,其速度v2,根据库仑定律,及牛顿第二定律,则有:加速度a2=$\frac{{F}_{2}}{m}$=$\frac{k\frac{Qq}{{r}_{2}^{2}}}{\frac{kQq}{{a}_{1}{r}_{1}^{2}}}$=$\frac{{a}_{1}{r}_{1}^{2}}{{r}_{2}^{2}}$;
(2)根据能量守恒定律,则有:$\frac{1}{2}m{v}_{1}^{2}+\frac{kQq}{{r}_{1}}=\frac{1}{2}m{v}_{2}^{2}+\frac{kQq}{{r}_{2}}$;
解得:v2=$\sqrt{{v}_{1}^{2}+\frac{2{a}_{1}{r}_{1}({r}_{2}-{r}_{1})}{{r}_{2}}}$;
而$m\frac{{v}_{1}^{2}}{{r}_{1}}=\frac{kQq}{{r}_{1}^{2}}$,
因此v2=$\sqrt{\frac{3{a}_{1}{r}_{1}{r}_{2}-2{a}_{1}{r}_{1}^{2}}{{r}_{2}}}$;
根据动能转化为电势能时,两者间距即为金原子核的半径,即为:$\frac{1}{2}{m}_{α}{v}_{0}^{2}=\frac{kQq}{r}$;
解得:r=$\frac{2kQq}{{m}_{α}{v}_{0}^{2}}$;
因此金原子核的直径$\frac{4kQq}{{m}_{α}{v}_{0}^{2}}$;
答:(1)在距离这个金核r2时,其速度=$\sqrt{\frac{3{a}_{1}{r}_{1}{r}_{2}-2{a}_{1}{r}_{1}^{2}}{{r}_{2}}}$,加速度是$\frac{{a}_{1}{r}_{1}^{2}}{{r}_{2}^{2}}$;
(2)示金原子核的直径$\frac{4kQq}{{m}_{α}{v}_{0}^{2}}$.
点评 考查库仑定律与牛顿第二定律的应用,掌握动能与电势能的表达式内容,注意建立估算原子核的半径模型是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:高中物理 来源: 题型:解答题
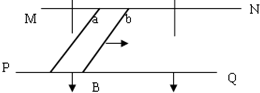 如图所示,足够长的相距为L的平行金属导轨MN、PQ放置在水平面内,匀强磁场竖直向下覆盖轨道平面,磁感应强度为B,在轨道上平行横放两根相距S0的金属导体棒a、b,使之与导轨构成矩形回路,每根金属棒的质量均为m,电阻均为R,导轨电阻可忽略,棒与导轨无摩擦,且不计重力和电磁辐射.开始时,导体棒a静止,导体棒b具有向右的初速度v0,最终两根金属棒会保持相对静止,求此时a、b棒之间的距离.
如图所示,足够长的相距为L的平行金属导轨MN、PQ放置在水平面内,匀强磁场竖直向下覆盖轨道平面,磁感应强度为B,在轨道上平行横放两根相距S0的金属导体棒a、b,使之与导轨构成矩形回路,每根金属棒的质量均为m,电阻均为R,导轨电阻可忽略,棒与导轨无摩擦,且不计重力和电磁辐射.开始时,导体棒a静止,导体棒b具有向右的初速度v0,最终两根金属棒会保持相对静止,求此时a、b棒之间的距离.查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:解答题

查看答案和解析>>
科目:高中物理 来源: 题型:解答题
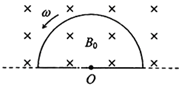 如图,均匀磁场中有一由半圆弧半径为L及其直径构成的导线框,半圆直径与磁场边缘重合; 磁场方向垂直于半圆面(纸面)向里,磁感应强度大小为B0.使该线框由图示位置从静止开始绕过圆心O、垂直于半圆面的轴以角速度ω匀速转动半周,在线框中产生感应电流.
如图,均匀磁场中有一由半圆弧半径为L及其直径构成的导线框,半圆直径与磁场边缘重合; 磁场方向垂直于半圆面(纸面)向里,磁感应强度大小为B0.使该线框由图示位置从静止开始绕过圆心O、垂直于半圆面的轴以角速度ω匀速转动半周,在线框中产生感应电流.查看答案和解析>>
科目:高中物理 来源: 题型:选择题
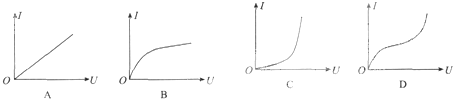
| A. | 10m/s | B. | 20m/s | C. | 25m/s | D. | 50m/s |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
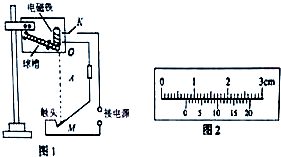 如图1,竖直平面内固定一斜槽,斜槽中放有若干个直径均为d的相同小铁球,紧靠斜槽末端固定有电磁铁,闭合开关K,电磁铁吸住第一个小球,第二个小球处于斜槽末端被第一个小球阻挡而不落下.轻敲金属片M,M与触点分离,第一个小球从O点开始下落,M迅速恢复接触,电磁铁又吸住第二个小球,当第一个小球撞击M时,第二个小球又开始下落…
如图1,竖直平面内固定一斜槽,斜槽中放有若干个直径均为d的相同小铁球,紧靠斜槽末端固定有电磁铁,闭合开关K,电磁铁吸住第一个小球,第二个小球处于斜槽末端被第一个小球阻挡而不落下.轻敲金属片M,M与触点分离,第一个小球从O点开始下落,M迅速恢复接触,电磁铁又吸住第二个小球,当第一个小球撞击M时,第二个小球又开始下落…查看答案和解析>>
科目:高中物理 来源: 题型:填空题
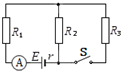 如图所示,电源电动势E=10V,内阻r=1Ω,R1=3Ω.电键S断开时,R2的功率为4W,电源的输出功率为4.75W,则电流表的读数为0.5A;电键S接通后,电流表的读数为2A.则R3=$\frac{16}{15}$Ω.
如图所示,电源电动势E=10V,内阻r=1Ω,R1=3Ω.电键S断开时,R2的功率为4W,电源的输出功率为4.75W,则电流表的读数为0.5A;电键S接通后,电流表的读数为2A.则R3=$\frac{16}{15}$Ω.查看答案和解析>>
科目:高中物理 来源: 题型:填空题
 如图所示,ab、bd、cd是竖直平面内三根固定的细杆,a、b、c、d位于同一圆周上,a点为圆周的最高点,d点为最低点.每根杆上都套着一个小滑环(图中末画出).三个滑环分别从a、b、c处释放(初速为0),用t1、t2、t3依次表示各滑环到达d点所用的时间,t1、t2、t3之间的关系为t1=t2=t3.
如图所示,ab、bd、cd是竖直平面内三根固定的细杆,a、b、c、d位于同一圆周上,a点为圆周的最高点,d点为最低点.每根杆上都套着一个小滑环(图中末画出).三个滑环分别从a、b、c处释放(初速为0),用t1、t2、t3依次表示各滑环到达d点所用的时间,t1、t2、t3之间的关系为t1=t2=t3.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com