
分析 (1)对第一次打击和第二次打击分别运用动能定理列式,求功时用的力平均值.
(2)再对第三次打击,运用动能定理列式,发现规律,得到打击第六次铁桩进入泥土的深度.
(3)运用归纳法,得到打击第n-1次,第n次铁桩进入泥土的深度.
解答 解:第一解法:设打击第一次铁桩泥土的深度为l1=20×10-2m=0.2m,打击两次铁桩进入泥土的深度为l2,打击三次铁桩泥土的深度为l3,…;泥土对铁桩的阻力为f=kl;每打击一次由重垂势能转化给铁桩的动能对泥土所做的功为W,根据题目所给定的条件,每次打击都是相同的.由动能定理,则可有下列各式:
(1)打击第一次铁桩时,有:W=$\frac{1}{2}$f1l1=$\frac{1}{2}$kl12
有:l1=$\sqrt{\frac{2W}{k}}$=0.2m…①
打击二次铁桩时,有:2W=$\frac{1}{2}$f2l2=$\frac{1}{2}$kl22
有:l2=2$\sqrt{\frac{W}{k}}$=0.2$\sqrt{2}$m…②
所以,打击第二次铁桩进入泥土的深度为:
△l1=l2-l1=0.2($\sqrt{2}$-1)m=8.28×10-2m.
(2)由前面的①②式我们可以得到:
3W=$\frac{1}{2}$f3l3=$\frac{1}{2}$kl32 有:l3=$\sqrt{\frac{6W}{k}}$=0.2$\sqrt{3}$m…③
(n-1)W=$\frac{1}{2}$f(n-1)l(n-1)=$\frac{1}{2}$kln-12 有:l(n-1)=$\sqrt{\frac{2(n-1)W}{k}}$=0.2$\sqrt{n-1}$m…④
nW=fn ln=k ln$_n^2$ 有:ln=$\sqrt{\frac{2nW}{k}}$=0.2$\sqrt{n}$ m…⑤
得到:△ln=($\sqrt{n}$-$\sqrt{n-1}$)l1…⑥
由(6)式,代入问题②的条件有:△l6=0.2×($\sqrt{6}$-$\sqrt{6-1}$)m=4.27×10-2m
所以,打击第六次铁桩进入泥土的深度为:4.27×10-2m.
(3)同理对于第n次打击铁桩进入泥土的深度△ln=($\sqrt{n}$-$\sqrt{n-1}$)l1=0.2($\sqrt{n}$-$\sqrt{n-1}$) m
第二解法:根据题意,铁桩每次对泥土所做的功相同,铁桩所受阻力是与进入的深度成正比的,则阻力是f-l图中通过原点的一条斜线,如图1所示.斜线与l 轴所围成的“面积”,就是阻力所做的功,“W”是每打击一次铁桩克服阻力所做的功.根据相似直角三角形的性质,其面积之比等于某一直角边的平方比.则打击一次、打击两次、打击三次、…打击n次铁桩进入泥土的深度之比为:
l1:l2:l3:…ln-1:ln=1:$\sqrt{2}$:$\sqrt{3}$…$\sqrt{n-1}$:$\sqrt{n}$.
所以,得到打击第二次铁桩进入泥土的深度为:
△l1=l2-l1=($\sqrt{2}$-1)l1=($\sqrt{2}$-1)20×10-2m=8.28×10-2m.
同理,打击第六次铁桩进入泥土的深度为:△l6=($\sqrt{6}$-$\sqrt{5}$)20×10-2m=4.27×10-2m
第n次打击铁桩进入泥土的深度为:△ln=($\sqrt{n}$-$\sqrt{n-1}$)l1.
答:(1)打击第二次铁桩进入泥土的深度是8.28×10-2m.
(2)打击第六次铁桩进入泥土的深度是4.27×10-2m.
(3)打击第n次铁桩进入泥土的深度是0.2($\sqrt{n}$-$\sqrt{n-1}$)m.
点评 本题所考查的是应用数学工具解决物理问题的能力.用数学图象法解答打桩问题,不仅使解答过程简化,且从图象中反映的物理量的关系也很清楚,这样有利用理解题目的物理意义.


 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:高中物理 来源: 题型:解答题

查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 10m/s2 | B. | 5m/s2 | C. | 3m/s2 | D. | 7m/s2 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
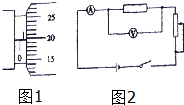 在“测定金属丝电阻率”的实验中,需要测出其长度L,直径d和电阻R.
在“测定金属丝电阻率”的实验中,需要测出其长度L,直径d和电阻R.查看答案和解析>>
科目:高中物理 来源: 题型:选择题

| A. | 物体动能损失了 $\frac{mgh}{2}$ | B. | 物体动能损失了2mgh | ||
| C. | 系统机械能损失了2mgh | D. | 系统机械能损失了$\frac{mgh}{2}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 我国的“嫦娥三号”探月卫星将于2013年下半年择机发射.“嫦娥三号”卫星将实验“月面软着陆”.该过程的最后阶段是:着陆器离月球表面几米高时速度减小为零,为防止发动机将月球表面上的尘埃吹起,此时要关掉所有的发动机,让着陆器自由下落着陆,假设下落高度为h,测得下落经历时间为t.试求:
我国的“嫦娥三号”探月卫星将于2013年下半年择机发射.“嫦娥三号”卫星将实验“月面软着陆”.该过程的最后阶段是:着陆器离月球表面几米高时速度减小为零,为防止发动机将月球表面上的尘埃吹起,此时要关掉所有的发动机,让着陆器自由下落着陆,假设下落高度为h,测得下落经历时间为t.试求:查看答案和解析>>
科目:高中物理 来源: 题型:多选题
 如图所示,轻质弹簧的一端与固定的竖直板P栓接,弹簧处于原长,另一端与物体A相连,物体A置于光滑水平桌面上(桌面足够大、足够高),A右端连接一水平细线,细线绕过光滑的定滑轮与物体B相连,A、B质量都为m,开始时托住物体B,让A处于静止且细线恰好伸直,然后由静止释放B,B下落h1时获得最大速度v,B下落h2时到达最低点,下列有关该过程的分析中正确的是( )
如图所示,轻质弹簧的一端与固定的竖直板P栓接,弹簧处于原长,另一端与物体A相连,物体A置于光滑水平桌面上(桌面足够大、足够高),A右端连接一水平细线,细线绕过光滑的定滑轮与物体B相连,A、B质量都为m,开始时托住物体B,让A处于静止且细线恰好伸直,然后由静止释放B,B下落h1时获得最大速度v,B下落h2时到达最低点,下列有关该过程的分析中正确的是( )| A. | B物体在最低点时受到细线的拉力大于B的重力 | |
| B. | 下落过程中,B物体机械能的减少量大于弹簧弹性势能的增加量 | |
| C. | A和B物体动能的增加量等于B物体重力对B做的功与弹簧弹力对A做的功之和 | |
| D. | B物体下落h1时弹簧的弹性势能为mgh1-$\frac{1}{2}$mv2 |
查看答案和解析>>
科目:高中物理 来源: 题型:填空题

查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 跳伞运动员从某高度的直升机上跳下,经过2s拉开绳索开启降落伞,此后再过18s落地.整个跳伞过程中的v-t图象如图所示.根据图象信息可知( )
跳伞运动员从某高度的直升机上跳下,经过2s拉开绳索开启降落伞,此后再过18s落地.整个跳伞过程中的v-t图象如图所示.根据图象信息可知( )| A. | 4s末速度为16m/s | |
| B. | 前2s跳伞运动员只受重力作用 | |
| C. | 第10s秒初速度大于0-2s内的平均速度 | |
| D. | 跳伞运动员下落的总高度约为250m |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com