
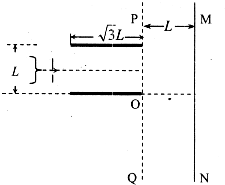
 ��ͼ��ʾ��-����ǹ�У�����Ϊ�������Ϊ�����ӣ������ٵ糡�Ӿ�ֹ���ٺ��γ�ˮƽ��������Ӽ�������ˮƽ���õ�ƽ�н�����䣬��֪�����峤Ϊ������ΪL��������ѹΪU����������������������룬����������Ҫʹ���ӽ���糡�����½������ԵO���������
��ͼ��ʾ��-����ǹ�У�����Ϊ�������Ϊ�����ӣ������ٵ糡�Ӿ�ֹ���ٺ��γ�ˮƽ��������Ӽ�������ˮƽ���õ�ƽ�н�����䣬��֪�����峤Ϊ������ΪL��������ѹΪU����������������������룬����������Ҫʹ���ӽ���糡�����½������ԵO������������� ��1�������ڼ��ٵ糡�У����ö��ܶ����õ����ٵ�ѹ���ٶȵĹ�ϵ�����ӽ���ƫת�糡������ƽ���˶�����ţ�ٵڶ����ɺͷ�λ�ƹ�ʽ��ʽ�����������ٵ�ѹ��
��2�����ٶȵķֽ�������ӽ���ų�ʱ�ٶȷ������켣���ɼ��ι�ϵ���켣�뾶�������������ṩ���������Ÿ�Ӧǿ�ȵĴ�С�������ֶ����ж��䷽��
���  �⣺��1�������ڵ���ǹ�м��٣��ݶ��ܶ����ɵã�
�⣺��1�������ڵ���ǹ�м��٣��ݶ��ܶ����ɵã�
qU0=$\frac{1}{2}m{v}_{0}^{2}$ ��
���ӽ���ƫת�糡������ƽ���˶�����
x=$\sqrt{3}$L=v0t ��
y=$\frac{L}{2}$=$\frac{1}{2}a{t}^{2}$ ��
����ţ�ٵڶ����ɵ�
a=$\frac{qU}{mL}$ ��
�����٢ڢۢܵã�U0=1.5U ��
��2��������O�������������ˮƽ����ɦȽǣ�
�� y=$\frac{L}{2}$=$\frac{{v}_{y}}{2}t$ ��
�ԱȢڢã�vy=$\frac{\sqrt{3}}{3}{v}_{0}$ ��
�� tan��=$\frac{{v}_{y}}{{v}_{0}}$=$\frac{\sqrt{3}}{3}$����=30���
���ӽ���ų�ʱ���ٶ� v=$\frac{{v}_{0}}{cos��}$=$\frac{2\sqrt{3}}{3}{v}_{0}$ ��10��
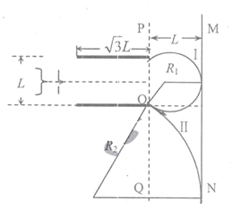
���ų�����ֱ��xOyƽ�����⣬��켣��ͼ�й켣����ʾ��
�������˶��İ뾶ΪR1���ɼ��ι�ϵ�ɵã�
R1+$\frac{{R}_{1}}{2}$=L
�� R1=$\frac{2}{3}$L ��11��
��ţ�ٵڶ����ɵã�qvB=m$\frac{{v}^{2}}{{R}_{1}}$ ��12��
B=$\frac{3}{L}\sqrt{\frac{mU}{q}}$
���ų�����ֱ��xOyƽ�������켣��ͼ�й켣����ʾ��
�������˶��İ뾶ΪR2���ɼ��ι�ϵ�ɵã�
R2-$\frac{{R}_{2}}{2}$=L ��13��
�ɵ� R2=2L
��qvB=m$\frac{{v}^{2}}{{R}_{2}}$��������� B=$\frac{1}{L}\sqrt{\frac{mU}{q}}$ ��14��
��
��1������ǹ�еļ��ٵ�ѹΪ1.5U��
��2���ų�����ֱ��xOyƽ������ʱ���Ÿ�Ӧǿ�ȵĴ�СΪ$\frac{3}{L}\sqrt{\frac{mU}{q}}$���ų�����ֱ��xOyƽ������ʱ���Ÿ�Ӧǿ�ȵĴ�СΪ$\frac{1}{L}\sqrt{\frac{mU}{q}}$��
���� ���������˴��������ڴų��к͵糡���˶��о������IJ�ͬ���ڴų���������Բ���˶��������켣���ɼ���֪ʶ��������ǻ����������������ڵ糡����ƽ���˶����˶��ķֽ��dz���˼·��


 һ���㶨ϵ�д�
һ���㶨ϵ�д� ��У��ҵ��ϵ�д�
��У��ҵ��ϵ�д� ���ɶ���ܲ��¿�ֱͨ��Уϵ�д�
���ɶ���ܲ��¿�ֱͨ��Уϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
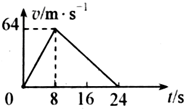 һ����̽���������ڵ����DZ�����ֱ���գ����չ�����ijʱ�̹رշ����������ٶ�ʱ��ͼ����ͼ��ʾ����֪�����DZ���û�п�����̽������������ʱ�����������㶨��̽������������Ϊ1.5��103kg����̽�������յķ�Χ�������������ٶȿ���Ϊ���䣮��
һ����̽���������ڵ����DZ�����ֱ���գ����չ�����ijʱ�̹رշ����������ٶ�ʱ��ͼ����ͼ��ʾ����֪�����DZ���û�п�����̽������������ʱ�����������㶨��̽������������Ϊ1.5��103kg����̽�������յķ�Χ�������������ٶȿ���Ϊ���䣮���鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
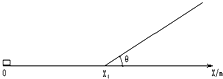 ������ˮƽ���ϴ�X������ԭ��O��V0=20m/s�ij��ٶ���X��������ʼ�˶�����X1=20m������һ�����Ϊ45���б�棬�ֻ�������������ÿ�ξ���б���ʱ������ʧ��е�ܣ���֪��Ħ��������Ϊ��=0.50��gȡ10m/s2��������ֹͣ�˶�ʱλ�õ����꣮��������������λ��Ч���֣�
������ˮƽ���ϴ�X������ԭ��O��V0=20m/s�ij��ٶ���X��������ʼ�˶�����X1=20m������һ�����Ϊ45���б�棬�ֻ�������������ÿ�ξ���б���ʱ������ʧ��е�ܣ���֪��Ħ��������Ϊ��=0.50��gȡ10m/s2��������ֹͣ�˶�ʱλ�õ����꣮��������������λ��Ч���֣��鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
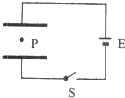 ��ͼ��ʾ��ƽ�а��������ֱ����ԴE����������S�պ�ʱ��һ�����͵�λ�ڵ������е�P��ǡ�ô���ƽ��״̬������˵����ȷ���ǣ�������
��ͼ��ʾ��ƽ�а��������ֱ����ԴE����������S�պ�ʱ��һ�����͵�λ�ڵ������е�P��ǡ�ô���ƽ��״̬������˵����ȷ���ǣ�������| A�� | �͵δ����� | |
| B�� | �͵δ����� | |
| C�� | ���ֿ���S�պϣ����������������֮��ľ��룬�͵ν������˶� | |
| D�� | ��������S�Ͽ�����С������������֮��ľ��룬�͵ν������˶� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
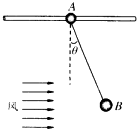 ��ͼ��ʾ��ˮƽϸ������һA����A����B�����һ�����������������ֱ�ΪmA��mB������B���ܵ��������ã�A����B��һ�����������˶�����֪ϸ������ֱ����ļн�Ϊ�ȣ�������˵������ȷ���ǣ�������
��ͼ��ʾ��ˮƽϸ������һA����A����B�����һ�����������������ֱ�ΪmA��mB������B���ܵ��������ã�A����B��һ�����������˶�����֪ϸ������ֱ����ļн�Ϊ�ȣ�������˵������ȷ���ǣ�������| A�� | B���ܵ��ķ���F����mBgtan�� | |
| B�� | ��������ʱ����������B����������ֲ��� | |
| C�� | �˶�A����֧�������ŷ��������Ӷ����� | |
| D�� | A����ˮƽϸ�˼�Ķ�Ħ������Ϊ$\frac{{m}_{B}}{{m}_{A}+{m}_{B}}$ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | ���������Ϊm=$\frac{4{��}^{2}S}{G{{T}_{3}}^{2}}$ | B�� | ���������Ϊm=$\frac{4{��}^{2}S}{G{{T}_{1}}^{2}}$ | ||
| C�� | ������ܶ�Ϊ��=$\frac{3��S}{G{{T}_{1}}^{2}}$ | D�� | �����˶��ļ��ٶ�Ϊa=$\frac{4{��}^{2}S}{{{T}_{1}}^{2}}$ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | R��$\frac{{v}^{2}}{kg}$ | B�� | R��$\frac{{v}^{2}}{kg}$ | C�� | R��$\frac{2{v}^{2}}{kg}$ | D�� | R��$\frac{{v}^{2}}{2kg}$ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
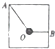 ��ͼ��ʾ��װ�ã�һ����Ϊm��С�����쳤������OA��OBϵס��������װ�ü����˶�ʱ������˵����ȷ���ǣ�������
��ͼ��ʾ��װ�ã�һ����Ϊm��С�����쳤������OA��OBϵס��������װ�ü����˶�ʱ������˵����ȷ���ǣ�������| A�� | ��������٣�OB������������Ϊ�� | |
| B�� | �����Ҽ��٣�OA������������Ϊ�� | |
| C�� | �����ϼ��٣�OB��������һ����Ϊ�� | |
| D�� | �����¼��٣�OA��OB��������������ͬʱΪ�� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com