
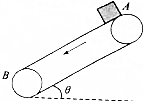
 ��ͼ��ʾ����ˮƽ��н�Ϊ��=37��Ĵ��ʹ��Ժ㶨����v=2m/s�˶���Ƥ��ʼ�ձ�����������Ϊm=1kg���������ط��ڴ��ʹ��ϵ�A��������1.2s���ﴫ�ʹ�B��������봫�ʹ��Ļ���Ħ������Ϊ��=0.5������Ħ�����ƣ����������ٶ�g=10m/s2��sin37��=0.6��cos37��=0.8������
��ͼ��ʾ����ˮƽ��н�Ϊ��=37��Ĵ��ʹ��Ժ㶨����v=2m/s�˶���Ƥ��ʼ�ձ�����������Ϊm=1kg���������ط��ڴ��ʹ��ϵ�A��������1.2s���ﴫ�ʹ�B��������봫�ʹ��Ļ���Ħ������Ϊ��=0.5������Ħ�����ƣ����������ٶ�g=10m/s2��sin37��=0.6��cos37��=0.8���������� ����A�ڴ��ʹ����ܵ���Ħ���������DZ���Ĺؼ����շ���ʱ���ڴ��ʹ��ٶȴ�A�ܵ�����Ħ������б�����£��������ٶ����ʱ���ڦ�mgcos37�㣼mgsin37�㣬���Դ�ʱĦ������б�����ϣ���������ͬ���������в�ͬ���ٶȣ��ٸ���ţ���˶����ɺ��˶�ѧ������⣮
��� �⣺��1���շ��ϴ��ʹ�ʱֱ���봫�ʹ��ٶ���ͬ����������mgsin37��+��mgcos37��=ma
�������ݵõ���a=10m/s2
�ﵽ�봫�ʹ��ٶ���ͬ��ʱ��
${t}_{1}=\frac{v}{a}$=$\frac{2m/s}{10m/{s}^{2}}=0.2s$
���ʱ�������λ��
${x}_{1}=\frac{1}{2}a{t}^{2}$=$\frac{10��0��{2}^{2}}{2}m=0.2m$
��2��֮���������Ħ����С���������»���������������������¼��٣�
��ʱ�������� mgsin37��-��mgcos37��=ma2
�����ã�${a}_{2}=2m/{s}^{2}$
�������پ�����t2=t��-t1=1s ���ʱ���������λ�ƣ�
${x}_{2}=v{t}_{2}+\frac{1}{2}{a}_{2}{{t}_{2}}^{2}$=$2m/s��1s+\frac{2m/{s}^{2}����1s��^{2}}{2}=2m+1m=3m$
����B����ٶ�Ϊ��
vB=v+a2t=2m/s+2��2m/s=4m/s
���ʹ��ij���Ϊ��
L=x1+x2=0.2m+3m=3.2m
�𣺣�1��������봫�ʹ��ٶ���ͬʱ������˶���ʱ��Ϊ0.2s��λ�ƵĴ�СΪ0.2m
��2�����ʹ��ij���Ϊ3.2m����鵽�ﴫ�ʹ�B���ٶȵĴ�С4m/s
���� ����ȿ���ţ���˶��������˶�ѧ���ɵ��ۺϣ��ֿ�����Ħ�������ѵ㣬�ر�ע����������Ħ�����������˱仯��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
 ��ͼ��ʾ�Ǽ�ʽǧ�ﶥ����ҡ������ʱ�������������ʹǧ�ﶥ�����ۿ�£���Ӷ����������𣮵����ָձ�����ʱ������ǧ�ﶥ��ѹ��Ϊ1.0��105N����ʱǧ�ﶥ���ۼ�ļн�Ϊ120�㣬�������ж���ȷ���ǣ�������
��ͼ��ʾ�Ǽ�ʽǧ�ﶥ����ҡ������ʱ�������������ʹǧ�ﶥ�����ۿ�£���Ӷ����������𣮵����ָձ�����ʱ������ǧ�ﶥ��ѹ��Ϊ1.0��105N����ʱǧ�ﶥ���ۼ�ļн�Ϊ120�㣬�������ж���ȷ���ǣ�������| A�� | ��ʱ�����ܵ���ѹ����С��Ϊ5.0��104N | |
| B�� | ��ʱǧ�ﶥ��������֧����Ϊ2.0��105N | |
| C�� | ������ҡ�����֣����������������ܵ���ѹ�������� | |
| D�� | ������ҡ�����֣����������������ܵ���ѹ������С |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
| A�� | $\frac{x_1}{{{t_1}^2}}=\frac{x_2}{{{t_2}^2}}=\frac{x_3}{{{t_3}^2}}$ | B�� | $\frac{x_1}{t_1}��\frac{x_2}{t_2}��\frac{x_3}{t_3}$ | ||
| C�� | $\frac{x_1}{t_1}=\frac{x_2}{t_2}=\frac{x_3}{t_3}$ | D�� | $\frac{x_1}{{{t_1}^2}}��\frac{x_2}{{{t_2}^2}}��\frac{x_3}{{{t_3}^2}}$ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�������
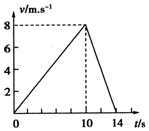 һ�����ɾ�ֹ��ʼ�˶����ٶ�-ʱ���ϵͼ����ͼ����
һ�����ɾ�ֹ��ʼ�˶����ٶ�-ʱ���ϵͼ����ͼ�����鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�������
 ��ͼ��ʾ����һ�㹻��������ڣ���һ��ֱֽ���������ǿ�ų����Ÿ�Ӧǿ��B=0.25T������һˮƽ���ҵ���ǿ�糡����ǿE=2��102N/C��һ����СҺ������m=$\sqrt{3}$��10-5kg�������q=-5��10-7C���ڴ�����ǡ����ֱ���˶���ȡg=10m/s2���˴���Һ���˶��ٶȵĴ�С���ٶȷ�����糡ǿ�ȷ���ļнǣ�
��ͼ��ʾ����һ�㹻��������ڣ���һ��ֱֽ���������ǿ�ų����Ÿ�Ӧǿ��B=0.25T������һˮƽ���ҵ���ǿ�糡����ǿE=2��102N/C��һ����СҺ������m=$\sqrt{3}$��10-5kg�������q=-5��10-7C���ڴ�����ǡ����ֱ���˶���ȡg=10m/s2���˴���Һ���˶��ٶȵĴ�С���ٶȷ�����糡ǿ�ȷ���ļнǣ��鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
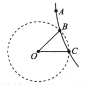 ��ͼ��ʾ���ڵ�O����һ�������ɣ��ڹ���O����ֱƽ���ڵĵ�A�������ͷ�һ���������С��С�������Ϊm��������Ϊq��С�����µĹ켣��ͼ�е�ʵ����ʾ�������Ե�OΪԲ�ģ�RΪ�뾶��Բ��ͼ��������ʾ���ཻ��B��C���㣬��O��C��ͬһˮƽ���ϣ���BOC=30�㣬��A��OC�ĸ߶�Ϊh����С��ͨ��B����ٶ�Ϊv��������
��ͼ��ʾ���ڵ�O����һ�������ɣ��ڹ���O����ֱƽ���ڵĵ�A�������ͷ�һ���������С��С�������Ϊm��������Ϊq��С�����µĹ켣��ͼ�е�ʵ����ʾ�������Ե�OΪԲ�ģ�RΪ�뾶��Բ��ͼ��������ʾ���ཻ��B��C���㣬��O��C��ͬһˮƽ���ϣ���BOC=30�㣬��A��OC�ĸ߶�Ϊh����С��ͨ��B����ٶ�Ϊv��������| A�� | С���˶���C��ʱ���ٶ�Ϊ$\sqrt{{v}^{2}+g��h-\frac{R}{2}��}$ | |
| B�� | С���˶���C����ٶ�Ϊ$\sqrt{{v}^{2}+gR}$ | |
| C�� | С���A���˶���C��Ĺ����е糡�������Ĺ�Ϊ$\frac{1}{2}$mv2-mg��h-$\frac{R}{2}$�� | |
| D�� | С���A���˶���C��Ĺ����е糡�������Ĺ�Ϊ$\frac{1}{2}$mv2-mgh |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ʵ����
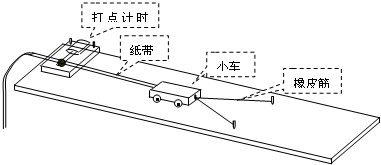
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
 ��ͼ��ʾ�������������������ֱ�ҵȸߵ�ˮƽ���ʹ����ң��ٶȺ㶨���䣩�����ٶ�Ϊv0�������뿪��ǰ����ٶ���ͬ����ƽ�ȵش������ϣ��ҵ��ٶ�ҲΪv0����������֮��Ķ�Ħ������Ϊ�̣��������ٶ�Ϊ g�����ҵĿ����㹻������˵����ȷ�ģ�������
��ͼ��ʾ�������������������ֱ�ҵȸߵ�ˮƽ���ʹ����ң��ٶȺ㶨���䣩�����ٶ�Ϊv0�������뿪��ǰ����ٶ���ͬ����ƽ�ȵش������ϣ��ҵ��ٶ�ҲΪv0����������֮��Ķ�Ħ������Ϊ�̣��������ٶ�Ϊ g�����ҵĿ����㹻������˵����ȷ�ģ�������| A�� | ����ջ����Ҵ��ʹ�ʱ���ܵ�Ħ������СΪ��mg | |
| B�� | ����ջ����Ҵ��ʹ�ʱ���ܵ�Ħ������СΪ$\sqrt{2}$��mg | |
| C�� | ���������ϲ��� ��ֱ���ҵ��˶����� �����ľ���Ϊ$\frac{\sqrt{2}{{v}_{0}}^{2}}{2��g}$ | |
| D�� | ���������ϲ��� ��ֱ���ҵ��˶����� �����ľ���Ϊ$\frac{\sqrt{2}{{v}_{0}}^{2}}{��g}$ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
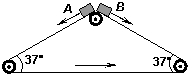 ��ͼ��ʾ�������δ��ʹ���1m/s���ٶ���ʱ�������˶������ߵĴ��ʹ�������2m������ˮƽ����ļнǾ�Ϊ37�㣮������С���A��B�Ӵ��ʹ����˶���1m/s�ij��ٶ��ش��ʹ��»�������봫�ʹ���Ķ�Ħ����������0.5����gȡ10m/s2��sin37��=0.6��cos37��=0.8������˵������ȷ���ǣ�������
��ͼ��ʾ�������δ��ʹ���1m/s���ٶ���ʱ�������˶������ߵĴ��ʹ�������2m������ˮƽ����ļнǾ�Ϊ37�㣮������С���A��B�Ӵ��ʹ����˶���1m/s�ij��ٶ��ش��ʹ��»�������봫�ʹ���Ķ�Ħ����������0.5����gȡ10m/s2��sin37��=0.6��cos37��=0.8������˵������ȷ���ǣ�������| A�� | ���A�ȵ��ﴫ�ʹ��� | |
| B�� | ���A��Bͬʱ���ﴫ�ʹ��� | |
| C�� | ���ʹ������A��B�������� | |
| D�� | ���A��B���ʹ��ϵĻ��۳���֮��Ϊ1��3 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com