

���� ����ʱ������ԭ����Ӧ�ӽ�����Դ��ÿ��0.02s��һ�ε㣮
ÿ5��������ȡ1�������㣬������������������֮���ʱ��Ϊ0.1s��
�����ȱ���ֱ���˶���ʱ���е���ٶȵ��ڸù����е�ƽ���ٶȣ����������ֽ����1��ʱС����˲ʱ�ٶȴ�С��
��� �⣺����ʱ��Ӧ���ڽ�����Դ�ϣ�ÿ��0.02s��һ�ε㣻
ÿ5��������ȡ1�������㣬������������������֮���ʱ��T=0.1s
�����ȱ���ֱ���˶����м�ʱ�̵��ٶȵ��ڸù����е�ƽ���ٶ�
���ԣ�v1=$\frac{{s}_{2}}{2T}$=$\frac{7.50��1{0}^{-2}}{0.2}$m/s=0.375m/s
�ʴ�Ϊ��������0.02��0.1��0.375��
���� �����ȱ���ֱ�ߵĹ����Լ����۽��ʵ���������������ƽʱ��ϰ��Ҫ��ǿ����֪ʶ��������Ӧ�ã���߽������������ע��������3λ��Ч���֣�


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ�ʵ����

�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
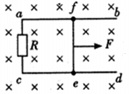 ��ͼ��ʾ�����L=0.4m�������⻬��ƽ�н�������ab��cd���̶��ھ�Եˮƽ���ϣ��������������һ����ֵR=0.4���Ķ�ֵ���裬����ĵ��費�ƣ�����һ����ҲΪL=0.4m�Ľ�����ef��ֱ����ڵ���ab��cd�ϣ�������ef�����r=0.1�����Ÿ�Ӧǿ��B=0.1T����ǿ�ų���ֱ�ڵ���ƽ�森����һˮƽ��F�����ڽ�����ef���е㣬����ˮƽ������v=5m/s���ٶ��������˶�ʱ����
��ͼ��ʾ�����L=0.4m�������⻬��ƽ�н�������ab��cd���̶��ھ�Եˮƽ���ϣ��������������һ����ֵR=0.4���Ķ�ֵ���裬����ĵ��費�ƣ�����һ����ҲΪL=0.4m�Ľ�����ef��ֱ����ڵ���ab��cd�ϣ�������ef�����r=0.1�����Ÿ�Ӧǿ��B=0.1T����ǿ�ų���ֱ�ڵ���ƽ�森����һˮƽ��F�����ڽ�����ef���е㣬����ˮƽ������v=5m/s���ٶ��������˶�ʱ�����鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
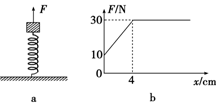 ��ͼa��ʾ��һ���ʵ��ɵ��¶˹̶���ˮƽ���ϣ��϶˷���һ���壨�����뵯�ɲ����ӣ�����ʼʱ���崦�ھ�ֹ״̬��������ֱ���ϵ�����F�����������ϣ�ʹ���忪ʼ�������ȼ����˶�������F������λ��x�Ĺ�ϵ��ͼb��ʾ��g=10m/s2��������ȷ�Ľ����ǣ�������
��ͼa��ʾ��һ���ʵ��ɵ��¶˹̶���ˮƽ���ϣ��϶˷���һ���壨�����뵯�ɲ����ӣ�����ʼʱ���崦�ھ�ֹ״̬��������ֱ���ϵ�����F�����������ϣ�ʹ���忪ʼ�������ȼ����˶�������F������λ��x�Ĺ�ϵ��ͼb��ʾ��g=10m/s2��������ȷ�Ľ����ǣ�������| A�� | �����뵯�ɷ���ʱ�����ɴ���ѹ��״̬ | |
| B�� | ����ļ��ٶȴ�СΪ5m/s2 | |
| C�� | ���������Ϊ2kg | |
| D�� | ���ɵľ���ϵ��Ϊ7.5N/cm |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
 �ס�������ijʱ����ͬһ�ص㣬��ͬһ����ʼ��ֱ���˶������Ը�ʱ����Ϊ��ʱ��㣬�õ�������λ��-ʱ��ͼ����ͼ��ʾ��ͼ���е�OC����ABƽ�У�CB����OAƽ�У�������˵������ȷ���ǣ�������
�ס�������ijʱ����ͬһ�ص㣬��ͬһ����ʼ��ֱ���˶������Ը�ʱ����Ϊ��ʱ��㣬�õ�������λ��-ʱ��ͼ����ͼ��ʾ��ͼ���е�OC����ABƽ�У�CB����OAƽ�У�������˵������ȷ���ǣ�������| A�� | t1��t2ʱ�������ľ���Խ��ԽԶ | |
| B�� | 0��t3ʱ���ڼ׳���ƽ���ٶȵ����ҳ���ƽ���ٶ� | |
| C�� | �׳��ij��ٶȵ����ҳ���t3ʱ�̵��ٶ� | |
| D�� | t3ʱ�̼׳����ҳ���ǰ�� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | �����ļ��ٶ�Ϊ2m/s2 | B�� | �����ļ��ٶ�Ϊ8m/s2 | ||
| C�� | ������ƽ���ٶ�Ϊ6m/s | D�� | ������ƽ���ٶ�Ϊ8m/s |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
 ��ͼ��ʾ��abcdΪˮƽ���õ�ƽ�й⻬�������죬������Ϊl�����費�ƣ�������д�ֱ�ڵ���ƽ�����ǿ�ų����Ÿ�Ӧǿ�ȴ�СΪB�������˷����ڵ����ϣ��뵼��ĽӴ���ΪM��N�����뵼��ɦȽǣ��������Ԧ� �Ľ��ٶ���N����ͼʾλ������ת�����뵼��ab��ֱ��ת�����̽������뵼��ʼ�����ýӴ��������˵�λ���ȵĵ���Ϊr�����ڽ�����ת�������У�������
��ͼ��ʾ��abcdΪˮƽ���õ�ƽ�й⻬�������죬������Ϊl�����費�ƣ�������д�ֱ�ڵ���ƽ�����ǿ�ų����Ÿ�Ӧǿ�ȴ�СΪB�������˷����ڵ����ϣ��뵼��ĽӴ���ΪM��N�����뵼��ɦȽǣ��������Ԧ� �Ľ��ٶ���N����ͼʾλ������ת�����뵼��ab��ֱ��ת�����̽������뵼��ʼ�����ýӴ��������˵�λ���ȵĵ���Ϊr�����ڽ�����ת�������У�������| A�� | M��N���������� | |
| B�� | �������и�Ӧ�����ķ�������N����M | |
| C�� | ��·�и�Ӧ�����Ĵ�Сʼ��Ϊ$\frac{Bl��}{2r}$ | |
| D�� | ��·��ͨ���ĵ���Ϊ$\frac{Bl}{2rtan��}$ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
| A�� | �о��������ѹ������Ĺ�ϵ | |
| B�� | ���о��ų�ʱ������Ÿ��߶Դų��������� | |
| C�� | ̽���ų��Ե��������ù��� | |
| D�� | ���о����������е���ͨ�����������������ͨ������ĵ��������衢ʱ��Ĺ�ϵ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | h=$\frac{{{R^2}v_0^2}}{{2G{m_��}}}��T=2��R\sqrt{\frac{R}{{G{m_��}}}}$ | B�� | h=$\frac{{{R^2}v_0^2}}{{2G{m_��}}}��T=��R\sqrt{\frac{R}{{G{m_��}}}}$ | ||
| C�� | h=$\frac{{{R^2}v_0^{\;}}}{{G{m_��}}}��T=2��R\sqrt{\frac{R}{{G{m_��}}}}$ | D�� | h=$\frac{{{R^2}v_0^{\;}}}{{G{m_��}}}��T=��R\sqrt{\frac{R}{{G{m_��}}}}$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com