
分析 若击球点的高度小于某一值,那么无论水平速度多大,球不是触网就是出界,该高度的临界情况是球刚好不触网,刚好不越界,结合平抛运动的规律求出这个高度.
解答 解:设该队员应跳的最小高度为h,
球在网的两边运动的时间之比为$d:\frac{L}{2}$,
根据等时性,在竖直方向上有:$\frac{h-H}{h}=\frac{{d}^{2}}{(d+\frac{L}{2})^{2}}$,
解得h=$\frac{(d+\frac{L}{2})^{2}H}{(d+\frac{L}{2})^{2}-{d}^{2}}$.
答:该队员至少跳起的高度为$\frac{(d+\frac{L}{2})^{2}H}{(d+\frac{L}{2})^{2}-{d}^{2}}$.
点评 解决本题的关键知道平抛运动在水平方向和竖直方向上的运动规律,抓住临界状态,结合运动学公式灵活求解.


科目:高中物理 来源: 题型:填空题
 计算机上常用的“3.5英寸、1.44MB”软磁盘的磁道和扇区如图所示,磁盘上共有80个磁道(即80个不同半径的同心圆),每 个磁道分成18个扇区(每个扇区为$\frac{1}{18}$圆周),每个扇区可记 录512个字节.电动机使磁盘以300r/min匀速转动.磁头在读、写数据时是不动的.磁盘每转一圈,磁头沿半径方向跳动一个磁道.则一个扇区通过磁头所用的时间是$\frac{1}{90}$s.
计算机上常用的“3.5英寸、1.44MB”软磁盘的磁道和扇区如图所示,磁盘上共有80个磁道(即80个不同半径的同心圆),每 个磁道分成18个扇区(每个扇区为$\frac{1}{18}$圆周),每个扇区可记 录512个字节.电动机使磁盘以300r/min匀速转动.磁头在读、写数据时是不动的.磁盘每转一圈,磁头沿半径方向跳动一个磁道.则一个扇区通过磁头所用的时间是$\frac{1}{90}$s.查看答案和解析>>
科目:高中物理 来源: 题型:填空题
 质量为m,带电量为-q的粒子(不计重力),在匀强电场中的A点以初速度v0沿垂直于场强E的方向射入到电场中,已知粒子到达B点时的速度大小为2v0,A、B间距为d,如图所示.则A、B两点间的电势差为-$\frac{3m{v}_{0}^{2}}{2q}$;匀强电场的场强大小为$\frac{\sqrt{21}m{v}_{0}^{2}}{2qd}$,方向为向左.
质量为m,带电量为-q的粒子(不计重力),在匀强电场中的A点以初速度v0沿垂直于场强E的方向射入到电场中,已知粒子到达B点时的速度大小为2v0,A、B间距为d,如图所示.则A、B两点间的电势差为-$\frac{3m{v}_{0}^{2}}{2q}$;匀强电场的场强大小为$\frac{\sqrt{21}m{v}_{0}^{2}}{2qd}$,方向为向左.查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图所示,一质量为m的小球用长为l的细线悬挂在O′点,开始时悬线与竖直方向之间的夹角为θ=60°,某时刻让小球从静止开始释放,当小球运动到最低点B时,恰好炸成质量相等的甲、乙两块,其中甲脱离悬线水平向左做平抛运动,落到水平面上的D点,乙仍做圆周运动且刚好可以通过最高点C.已知O、B两点间的高度为h,重力加速度为g,炸药质量忽略不计,试计算O、D两点间的水平距离x.
如图所示,一质量为m的小球用长为l的细线悬挂在O′点,开始时悬线与竖直方向之间的夹角为θ=60°,某时刻让小球从静止开始释放,当小球运动到最低点B时,恰好炸成质量相等的甲、乙两块,其中甲脱离悬线水平向左做平抛运动,落到水平面上的D点,乙仍做圆周运动且刚好可以通过最高点C.已知O、B两点间的高度为h,重力加速度为g,炸药质量忽略不计,试计算O、D两点间的水平距离x.查看答案和解析>>
科目:高中物理 来源: 题型:填空题
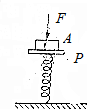 如图所示,轻弹簧的一端固定在地面上,另一端与轻木板P相连,质量为m的物体A固定在P上,竖直向下的力F作用在A上,A静止,若突然撤去力F,A运动到最高点时,弹簧对P的作用力为F-mg.
如图所示,轻弹簧的一端固定在地面上,另一端与轻木板P相连,质量为m的物体A固定在P上,竖直向下的力F作用在A上,A静止,若突然撤去力F,A运动到最高点时,弹簧对P的作用力为F-mg.查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 物体在万有引力场中具有的势能叫引力势能,若取两物体相距无穷远时的引力势能为零,一个质量为m0的质点距离质量为M0的引力源中心为r0时,其引力势能EP=-$\frac{G{M}_{0}{m}_{0}}{{r}_{0}}$(式中G为引力常数),如图所示,一颗质量为m的人造地球卫星在离地面高度为h的圆形轨道环绕地球飞行,已知地球的质量为M,地球的半径为R,以无穷远处引力势能为零,求:
物体在万有引力场中具有的势能叫引力势能,若取两物体相距无穷远时的引力势能为零,一个质量为m0的质点距离质量为M0的引力源中心为r0时,其引力势能EP=-$\frac{G{M}_{0}{m}_{0}}{{r}_{0}}$(式中G为引力常数),如图所示,一颗质量为m的人造地球卫星在离地面高度为h的圆形轨道环绕地球飞行,已知地球的质量为M,地球的半径为R,以无穷远处引力势能为零,求:查看答案和解析>>
科目:高中物理 来源: 题型:解答题
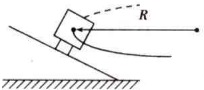 质量为m的火车以恒定的速率在水平面内沿一段半径为R的圆形轨道转弯,如图所示,已知路面有一定的倾角,当火车以速率v0在此晚到上转弯时,车轮对轨道的侧压力恰好为零,如果火车以实际速率v(v>v0)在此弯道上转弯时,侧车轮将施于铁轨一个与枕木平行的压力F,试求侧压力F的大小.
质量为m的火车以恒定的速率在水平面内沿一段半径为R的圆形轨道转弯,如图所示,已知路面有一定的倾角,当火车以速率v0在此晚到上转弯时,车轮对轨道的侧压力恰好为零,如果火车以实际速率v(v>v0)在此弯道上转弯时,侧车轮将施于铁轨一个与枕木平行的压力F,试求侧压力F的大小.查看答案和解析>>
科目:高中物理 来源: 题型:填空题
查看答案和解析>>
科目:高中物理 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com