
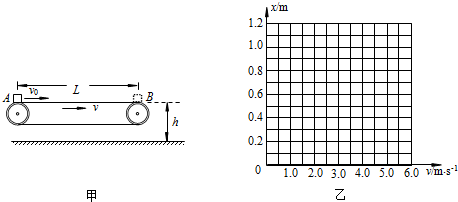
 如图1所示为车站使用的水平传送带的模型,它的水平传送带的长度为L=8m,传送带的皮带轮的半径均为R=0.2m,传送带的上部距地面的高度为h=0.45m,现有一个旅行包(视为质点),以v0=10m/s的初速度水平地滑上水平传送带,已知旅行包与皮带之间的动摩擦因数为μ=0.6.g取10m/s2,试讨论下列问题:
如图1所示为车站使用的水平传送带的模型,它的水平传送带的长度为L=8m,传送带的皮带轮的半径均为R=0.2m,传送带的上部距地面的高度为h=0.45m,现有一个旅行包(视为质点),以v0=10m/s的初速度水平地滑上水平传送带,已知旅行包与皮带之间的动摩擦因数为μ=0.6.g取10m/s2,试讨论下列问题: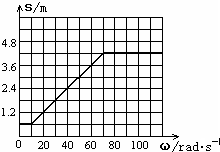 解:(1)旅行包做匀减速运动,a=μg=6m/s2
解:(1)旅行包做匀减速运动,a=μg=6m/s2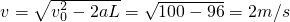
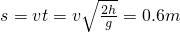 (m
(m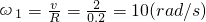
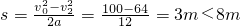 ;
;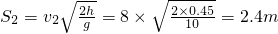
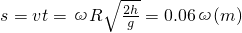


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中物理 来源: 题型:
查看答案和解析>>
科目:高中物理 来源: 题型:

查看答案和解析>>
科目:高中物理 来源: 题型:
 如图1所示为车站使用的水平传送带的模型,它的水平传送带的长度为L=8m,传送带的皮带轮的半径均为R=0.2m,传送带的上部距地面的高度为h=0.45m,现有一个旅行包(视为质点),以v0=10m/s的初速度水平地滑上水平传送带,已知旅行包与皮带之间的动摩擦因数为μ=0.6.g取10m/s2,试讨论下列问题:
如图1所示为车站使用的水平传送带的模型,它的水平传送带的长度为L=8m,传送带的皮带轮的半径均为R=0.2m,传送带的上部距地面的高度为h=0.45m,现有一个旅行包(视为质点),以v0=10m/s的初速度水平地滑上水平传送带,已知旅行包与皮带之间的动摩擦因数为μ=0.6.g取10m/s2,试讨论下列问题:查看答案和解析>>
科目:高中物理 来源: 题型:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com