

分析 (1)根据速度时间公式求出下滑和上滑的加速度大小,结合牛顿第二定律求出物块与杆之间的动摩擦因数.
(2)分段运用牛顿第二定律求得加速度,由位移速度关系公式求物块滑块的总路程和位移.也可以对全过程运用动能定理,求出物块滑块的总路程.
解答 解:(1)设杆子与水平方向的夹角为θ,由图象可知,物块匀加速运动的加速度大小 a1=$\frac{4}{1}$=4m/s2,匀减速上滑的加速度大小 a2=$\frac{4}{0.5}$=8m/s2
根据牛顿第二定律得:
下滑有 mgsinθ-μmgcosθ=ma1,
上滑有 mgsinθ+μmgcosθ=ma2,
联立两式解得 μ=0.25,sinθ=0.6
(2)由题可知,沿杆向下为正方向.t0=1s内物体向下位移:x0=$\frac{{v}_{0}}{2}{t}_{0}$=$\frac{4}{2}×1$=2m
t1=0.5s内物体向上的位移:x1=$\frac{{v}_{1}}{2}{t}_{1}$=$\frac{-4}{2}×0.5$=-1m
设向下通过x2位移内所用时间为t2,则x2=-x1=1m
由速度位移关系:v22=2a1x2,t2=$\frac{{v}_{2}}{{a}_{1}}$
代入数据可以得到:v2=2$\sqrt{2}$m/s,t2=0.5$\sqrt{2}$s.
由题可以知道,向上通过x3位移内用时t3,速度为v3,则v3=-v2=-2$\sqrt{2}$m/s
由速度位移关系:2a2x3=v32,t3=$\frac{{v}_{3}}{{a}_{2}}$
代入数据整理可以得到:x3=-0.5m,t3=0.25$\sqrt{2}$s.
由题可知,向下通过x4′位移内用时t4′,则x4′=-x3=0.5m,t4′=0.125s
则t0+t1+t2+t3+t4′=2.675s>2.5s,所用物块并未下滑至低部.
设物块下滑位移x4,时间 t4=2.5s-(t0+t1+t2+t3)=0.25s
x4=$\frac{1}{2}{a}_{1}{t}_{4}^{2}$=$\frac{1}{2}×4×0.2{5}^{2}$=0.125m
所以总位移为:x=x0+x1+x2+x3+x4=1.875m
总路程为:S=|x0|+|x1|+|x2|+|x3|+|x4|=4.375m
答:
(1)物块与杆之间的动摩擦因数μ是0.25;
(2)物块前2.5s内滑过的总路程s是4.375m,总位移x是1.875m.
点评 本题考查了牛顿第二定律以及运动学公式的综合运用,要知道加速度是联系力学和运动学的桥梁,学会分段研究物体的运动情况.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中物理 来源: 题型:选择题
| A. | 一对静摩擦力做功之和一定为零 | |
| B. | 一对滑动摩擦力做功之和一定为负值 | |
| C. | 当作用力做正功时,反作用力一定做负功 | |
| D. | 当作用力做正功时,反作用力可以做正功,也可以做负功,也可以不做功 |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
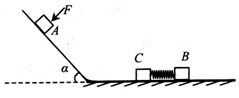 如图所示,粗糙的斜面与光滑的水平面通过半径可忽略的光滑小圆弧平滑连接.已知斜面的倾角α=45°,A、B、C是质量均为m=1kg的小滑块(均可视为质点),B和C用轻质弹簧连在一起.开始时,滑块B、C和弹簧均静止在水平面上.当滑块A置于斜面上且受到大小F=5$\sqrt{2}$N、方向垂直斜面向下的恒力作用时,恰能沿斜面向下匀速运动.现撤去F,让滑块A从斜面上距斜面底端L=10$\sqrt{2}$m处由静止下滑.取g=10m/s2.
如图所示,粗糙的斜面与光滑的水平面通过半径可忽略的光滑小圆弧平滑连接.已知斜面的倾角α=45°,A、B、C是质量均为m=1kg的小滑块(均可视为质点),B和C用轻质弹簧连在一起.开始时,滑块B、C和弹簧均静止在水平面上.当滑块A置于斜面上且受到大小F=5$\sqrt{2}$N、方向垂直斜面向下的恒力作用时,恰能沿斜面向下匀速运动.现撤去F,让滑块A从斜面上距斜面底端L=10$\sqrt{2}$m处由静止下滑.取g=10m/s2.查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | ${\;}_{36}^{89}$Kr中有89个核子 | |
| B. | Y原子核中含有56个中子 | |
| C. | 裂变时释放的能量为(m1-m2-m3-2m4)c2 | |
| D. | ${\;}_{92}^{235}$U的比结合能大于Y原子核的比结合能 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 物体加速下降,重力做正功 | |
| B. | 物体减速下降,重力做正功 | |
| C. | 摩擦力 f1 做正功,它的反作用力 f2 一定做负功 | |
| D. | 摩擦力 f1 做正功,它的反作用力 f2 可能不做功 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题

查看答案和解析>>
科目:高中物理 来源: 题型:选择题

| A. | 电压表的示数为6V | |
| B. | 通过电阻的电流方向1秒钟改变50次 | |
| C. | 在0.01s时刻,穿过线圈的磁通量最大 | |
| D. | 产生该交变电流的线圈在磁场中匀速转动的角速度为50π rad/s |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
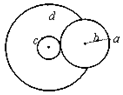 如图所示的靠轮传动(静摩擦力传动)装置中右轮半径为2r,a为它边缘上的一点,b为轮上的一点,b距轴为r.左侧为一轮轴(大小轮同步转动),大轮的半径为4r,d为它边缘上的一点,小轮的半径为r,c为它边缘上的一点.若传动中靠轮不打滑,则下列说法错误的是( )
如图所示的靠轮传动(静摩擦力传动)装置中右轮半径为2r,a为它边缘上的一点,b为轮上的一点,b距轴为r.左侧为一轮轴(大小轮同步转动),大轮的半径为4r,d为它边缘上的一点,小轮的半径为r,c为它边缘上的一点.若传动中靠轮不打滑,则下列说法错误的是( )| A. | b点与d点的线速度大小相等 | |
| B. | a点与c点的线速度大小相等 | |
| C. | c点与b点的角速度大小不相等 | |
| D. | a点与d点的向心加速度大小之比为1:8 |
查看答案和解析>>
科目:高中物理 来源: 题型:填空题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com