
本资料来源于《七彩教育网》http://www.7caiedu.cn
专题八《锐角三角函数与解直角三角形》
●中考点击
考点分析:
内容
要求
1、特殊角的三角函数值
Ⅰ
2、利用计算器求锐角的三角函数值,并能根据已知的三角函数值求对应的锐角
Ⅱ
3、综合运用三角函数解决与直角三角形有关的简单实际问题
Ⅱ
命题预测:本专题内容主要涉及两方面,一是锐角三角函数问题的基本运算,二是解直角三角形.其中,解直角三角形的应用题是中考重点考查的内容,题型广泛,有测建筑物高度的,有与航海有关的问题,有与筑路、修堤有关的问题.要注意把具体问题转化为数学模型,在计算时不能直接算出某些量时,要通过列方程的办法加以解决.
预测2007年中考的考查热点,主要要求能够正确地应用sinA、cosA、tgA、ctgA表示直角三角形两边的比,并且要熟记30°、45°、60°角的各个三角函数值.理解直角三角形中的边、角之间的关系,会用勾股定理及锐角三角函数解直角三角形,并会用相关的知识解决一些简单的实际问题,尤其是在计算距离、高度和角度等方面.
●难点透视
例1已知Rt△ABC中,∠C=90°,AC=2,BC=3,那么下列各式中,正确的是
【考点要求】本题考查锐角三角函数的概念。
【思路点拨】根据题目所给条件,可画出直角三角形,结合图形容易判断 是∠B的正切值。
是∠B的正切值。
【答案】选C。
【方法点拨】部分学生会直接凭想象判断并选择结果,从而容易导致错误。突破方法:这类题目本身难度不大,但却容易出现错误,关键是要画出图形,结合图形进行判断更具直观性,可减少错误的发生。
例2某山路坡面坡度 ,某人沿此山路向上前进
,某人沿此山路向上前进
【考点要求】本是考查坡度与坡角正切值关系。
【思路点拨】坡度 即坡角的正切值为
即坡角的正切值为 ,所以坡角的正弦值可求得等于
,所以坡角的正弦值可求得等于 ,所以沿着山路前进
,所以沿着山路前进 =10(米)。
=10(米)。
【答案】填10。
【方法点拨】少数学生因为未能正确理解坡度的意义,而出现使用错误。突破方法:牢记坡度 表示坡角的正切值即坡角的对边:坡角的邻边=
表示坡角的正切值即坡角的对边:坡角的邻边= ,然后再结合直角三角形,可求出坡角的正弦值,从而容易求得结果。
,然后再结合直角三角形,可求出坡角的正弦值,从而容易求得结果。
 例3如图8-1,在△ABC中,∠C=90°,点D在BC上,BD=4,AD=BC,cos∠ADC=
例3如图8-1,在△ABC中,∠C=90°,点D在BC上,BD=4,AD=BC,cos∠ADC= .求:(1)DC的长;(2)sinB的值.
.求:(1)DC的长;(2)sinB的值.
【考点要求】本题考查锐三角函数概念的相关知识及其简单运用。
【思路点拨】(1)∵在Rt△ABC中,cos∠ADC= =
= ,设CD=3k,∴AD=5k
,设CD=3k,∴AD=5k
又∵BC=AD,∴3k+4=5k,∴k=2. ∴CD=3k=6
【方法点拨】本题的关键是抓住“AD=BC”这一相等的关系,应用锐角三角函数的定义及勾股定理解题.
 例4如图所示,秋千链子的长度为
例4如图所示,秋千链子的长度为 ,则秋千踏板与地面的最大距离约为多少?(参考数据:
,则秋千踏板与地面的最大距离约为多少?(参考数据: ≈0.8,
≈0.8, ≈0.6)
≈0.6)
【考点要求】本题考查利用锐角三角函数知识和解直角三角形解决实际生活中的直角三角形问题.
【思路点拨】设秋千链子的上端固定于A处,秋千踏板摆动到最高位置时踏板位于B处.过点A,
B的铅垂线分别为AD,BE,点D,E在地面上,过B作BC⊥AD于点C.
【方法点拨】部分学生想直接求出踏板离地最高的距离即BE,但却缺少条件。突破方法:通过作辅助线,将BE转化到CD位置上,根据题目所给条件容易求出AC,从而可求得CD的长。
解题关键:利用解直角三角形求解实际问题的关键在于构造适当的直角三角形。
 例5如图8-5,一条渔船某时刻在位置A观测灯塔B、C(灯塔B距离A处较近),两个灯塔恰好在北偏东65°45′的方向上,渔船向正东方向航行l小时45分钟之后到达D点,观测到灯塔B恰好在正北方向上,已知两个灯塔之间的距离是12海里,渔船的速度是16海里/时,又知在灯塔C周围18.6海里内有暗礁,问这条渔船按原来的方向继续航行,有没有触礁的危险?
例5如图8-5,一条渔船某时刻在位置A观测灯塔B、C(灯塔B距离A处较近),两个灯塔恰好在北偏东65°45′的方向上,渔船向正东方向航行l小时45分钟之后到达D点,观测到灯塔B恰好在正北方向上,已知两个灯塔之间的距离是12海里,渔船的速度是16海里/时,又知在灯塔C周围18.6海里内有暗礁,问这条渔船按原来的方向继续航行,有没有触礁的危险?
【考点要求】本题考查解直角三角形在航海问题中的运用,解决这类问题的关键在于构造相关的直角三角形帮助解题.
∠BAD=90°-65°45′=24°15′.
AC=AB+BC=30.71+12=42.71(海里).
∴CE=AC?sin24°15′=42.71×0.4107=17.54(海里).
∵17.54<18.6,∴有触礁危险。
【答案】有触礁危险,不能继续航行。
【方法点拨】本题有两个难点,一是要能将实际问题抽象为数学问题,二是构造合适的直角形。突破方法:有无触礁危险,关键看离灯塔C最近的距离与18.6的大小关系,如果最近的距离大于18.6,则不会有触礁危险。
解题关键:离灯塔最近的距离是从灯塔向航线作垂线段。
例6某数学兴趣小组,利用树影测量树高.已测出树AB的影长AC为
(1)求出树高AB;
(2)因水土流失,此时树AB沿太阳光线方向倒下,在倾倒过程中,树影长度发生了变化,假设太阳光线与地面夹角保持不变,试求树影的最大长度.
(计算结果精确到 ≈1.414,
≈1.414,
 ≈1.732)
≈1.732)
 |
【考点要求】本题考查解直角三角形在测量中的实际运用.
【思路点拨】(1)在Rt△A BC中,∠BAC=90°,∠C=30°
(2)以点A为圆心,以AB为半径作圆弧,当太阳光线与圆弧相切时树影最长,点D为切点,DE⊥AD交AC于E点,(如图2)
在Rt△ADE中,∠ADE=90°,∠E=30°,
∴AE=2AD=2×5.2=10.4(米)
【答案】树高AB约为
【方法点拨】部分学生第(1)问没有太大困难,第(2)问中树在倾倒过程中,确定何处树影最长比较困难。突破方法:以A为圆心,AB为半径作圆弧,其中与圆弧相切的太阳光线所照射得到的树影最长。
解题关键:如何用直观的方式将树倾倒过程体现出来,这是解决该题的关键所在。
 例7初三(5)班综合实践小组去湖滨花园测量人工湖的长,如图
例7初三(5)班综合实践小组去湖滨花园测量人工湖的长,如图 ,结果精确到
,结果精确到
【考点要求】本题考查解直角三角形在实际生活当中的综合运用.要求学生能根据问题实际快速确定正确解决问题的方法.
【思路点拨】过点B作BE⊥D,BF⊥D,垂足分别为E,F,如图2
 由题意知,AD⊥CD
由题意知,AD⊥CD
∴四边形BFDE为矩形
∴BF=ED
在Rt△ABE中,AE=AB?cos∠EAB
在Rt△BCF中,BF=BC?cos∠FBC
∴AD=AE+BF=20?cos60o+40?cos45o
=10+20×1.414
=38.28(米)
【答案】
【方法点拨】部分学生知道需要利用解直角三角形来解题,但却又不知从何处入手。突破方法:在无法直接求出AD长的情况下,可考虑分段计算,也就是构造多个直角三角形,化整为零,各个突破,再积零为整,求得结果。
●难点突破方法总结
锐角三角函数与解直角三角形在近年的中考中,难度比以前有所降低,与课改相一致的是提高了应用的要求,强调利用解直角三角形知识解决生活实际中的有关测量、航海、定位等方面的运用。因此,在本专题中,有以下几点应加以注意。
1.正确理解锐三角函数的概念,能准确表达各三角函数,并能说出常用特殊角的三角函数值。
2.在完成锐角三角函数的填空、选择题时,要能根据题意画出相关图形,结合图形解题更具直观性。
3.能将实际问题转化为相关的直角三角形问题,即把实际问题抽象为几何问题,研究图形,利用数形结合思想、方程思想等解决生活问题。
4.注重基础,不断创新,掌握解直角三角形的基本技能,能灵活应对在测量、航海、定位等现代生活中常见问题,这也是以后中考命题的趋势。
●拓展练习
 一、填空题
一、填空题
3.如图,在甲、乙两地之间修一条笔直的公路,从甲地测得公路的走向是北偏东48°.甲、乙两地间同时开工,若干天后,公路准确接通,则乙地所修公路的走向是南偏西 度.
 |
|||
 |
|||
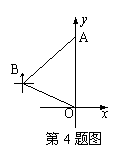
4.如图,机器人从A点,沿着西南方向,行了个4单位,到达B点后观察到原点O在它的南偏东60°的方向上,则原来A的坐标为 (结果保留根号).
5.求值:sin260°+cos260°= .
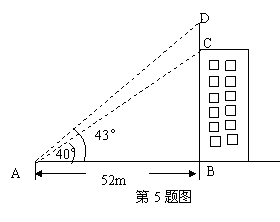 7.根据图中所给的数据,求得避雷针CD的长约为_______m(结果精确的到
7.根据图中所给的数据,求得避雷针CD的长约为_______m(结果精确的到
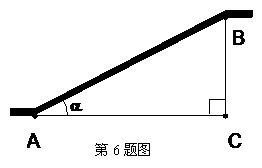 |
8.如图,自动扶梯AB段的长度为
二、选择题
9.在△ABC中,∠C=900,AC=BC=1,则tanA的值是( )
11.如图,梯子AB靠在墙上,梯子的底端A到墙根O的距离为 ,使梯子的底端
,使梯子的底端 到墙根O的距离等于
到墙根O的距离等于 ,那么
,那么 ( )
( )
A.等于
三、解答题
14.如图,河对岸有一铁塔AB.在C处测得塔顶A的仰角为30°,向塔前进
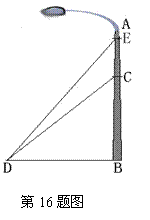 |
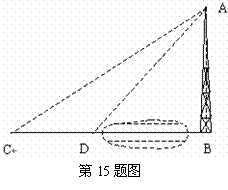
15.如图,我市某广场一灯柱AB被一钢缆CD固定,CD与地面成40°夹角,且DB=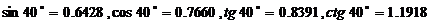 】
】
●习题答案
专题七《锐角三角函数与解直角三角形》
一、填空题
2.2.35
3.48(点拨:根据两直线平行,内错角相等判断)
7.4.86(点拨:利用正切函数分别求了BD,BC的长)
二、选择题
9. C
10.D
三、解答题
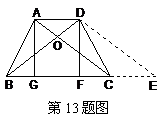
13.解:如图,作DE∥AC交BC的延长线于E,则四边形ACED是平行四边形.
∴AD=CE,DE=AC,易证△ABC≌△DCB
∴AC=DB,BD=DE
∴△DBE为等腰三角形
BE=BC+AD=
分别过A、D作AG⊥BC于G,DF⊥BC于F
∵∠BDE=∠BOC=1200,∴∠BDF=600
14.在Rt△ABD中,∵∠ADB=45°,∴BD=AB.
在R t△BCD中,BE=BC+CE= 6.20,
(若BC=4.1955暂不扣分,但是ED的长度未保留三个有效数字扣1分)
本资料由《七彩教育网》www.7caiedu.cn 提供!
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com