(1)该中学参加本次数学竞赛的有多少人? (2)如果90分以上(含90分)获奖,那么获奖率是多少? (3)这次竞赛成绩的中位数和众数分别落在哪个分数段内?
试题详情
20.(本题9分) 甲、乙两人在相同的条件下各射靶10次,每次命中的环数分别是: 甲:8, 6, 7, 8, 6, 5, 9, 10, 4, 7 ; 乙:6, 7, 7, 8, 6, 7, 8, 7, 9, 5 . (1)分别求甲、乙两人的平均数; (2)分别求出甲、乙两人的方差; (3)根据计算结果,估计两人谁发挥的较稳定? 试题详情
21.(本题9分) 某两个变量x和y之间的关系如下对应的数据: (精确到0.1) x 3 5 6 7 9 y 2 3 3 4 5 (1)画出散点图;
(2)求出回归方程; (3)若x=18,估计y的值. 试题详情
参考公式:回归直线的方程是: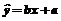 , , 试题详情
其中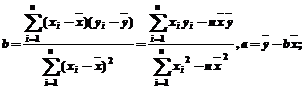 对应的回归估计值. 对应的回归估计值. 试题详情
22.(本题12分)设b和c分别是先后投掷一枚骰子得到的点数,关于x的一元二次方程x2+bx+c=0. 试题详情
(1)求方程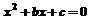 有实根的概率; 有实根的概率; 试题详情
(2)求在先后两次出现的点数中有5的条件下,方程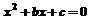 有实根的概率; 有实根的概率; (3)设f(x)=x2+bx+c(b,c∈R),b∈[1,4],c∈[2,4],求f(-2)>0成立时的概率。 试题详情
一.ADCDA, DBDAB, BA 二.13.1/20; 14. ;
15.3/10;
16.17/25 ;
15.3/10;
16.17/25 三.解答题: 17.解:由已知 <0, 则 <0, 则 是第三或第四象限角. ………………2分 是第三或第四象限角. ………………2分 当 是第三象限角时, 是第三象限角时,  , ,  ;………………5分 ;………………5分 当 是第四象限角时, 是第四象限角时,  , ,  .………………8分 .………………8分 18. 解:(1)0.7 ………………3分 (2) 0.6 ………………6分 (3) 他有可能是乘火车或轮船去, 他也有可能是乘汽车或飞机去. ………………9分 19.解:(Ⅰ)由直方图可知,参加本次竞赛的有: 4+6+8+7+5+2=32(人) ……………………3分 (Ⅱ)90分以上的人数为7+5=2=14(2分) ∴ 即本次竞赛获奖率是43.75% ………………6分 (Ⅲ)参赛同学共有32人,按成绩排序后,第16,17个数是最中间两个。 即中位数落在80~90之间 ; 由直方图,落在80~90之间的人数最多,共8人。 所以众数也落在80~90之间。……………………9分 20. 解:(1) ; ;
 . ……………………3分 . ……………………3分 (2)   ………………6分 ………………6分 (3)因 = = ; ;  ,所以乙发挥的较稳定. ……………………9分 ,所以乙发挥的较稳定. ……………………9分 21. 解:(1)略……………………3分 (2) ………………6分
………………6分 (3)当x=18时,  …………………9分 …………………9分 22.解:(b,c)的所有可能的取值有: (1,1), (1,2), (1,3), (1,4), (1,5), (1,6),
(2,1), (2,2), (2,3), (2,4), (2,5), (2,6), (3,1), (3,2), (3,3), (3,4), (3,5),
(3,6), (4,1), (4,2), (4,3), (4,4), (4,5), 4,6) ,(5,1), (5,2), (5,3), (5,4),
(5,5), (5,6), (6,1), (6,2), (6,3), (6,4), (6,5), (6,6), 共36种。…………3分 (1)要使方程x2+bx+c=0有实根,必须满足△=b2-4c≥0,符合条件的有: (2,1),
(3,1), (3,2), (4,1), (4,2), (4,3), (4,4), (5,1), (5,2), (5,3), (5,4), (5,5),
(5,6), (6,1), (6,2), (6,3), (6,4), (6,5), (6,6),共19种。 ∴
方程x2+bx+c=0有实根的概率为 。 ……………6分 。 ……………6分 (2)
先后两次出现的点数中有5的可能结果有:(1,5), (2,5), (3,5), (4,5), (5,1), (5,2), (5,3), (5,4), (5,5),
(5,6), (6,5), 共11种。其中使方程x2+bx+c=0有实根的结果有:(5,1), (5,2), (5,3), (5,4), (5,5), (5,6), (6,5), 共7种。 ∴在先后两次出现的点数中有5的条件下,方程x2+bx+c=0有实根的概率为 。…………9分 。…………9分 (3) 试验的全部结束所构成的区域为 . . 构成事件 的区域为 的区域为 . . 所以所求的概率为p . ……………………………12分www.ks5u.com . ……………………………12分www.ks5u.com
|

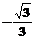 B.
B.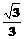 C.
C.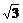 D.
D.