|
试题详情
2.如图,正三棱柱ABC―A1B1C1中,AB=AA1,
则AC1与平面BB1C1C所成的角的正弦值为 ( ) 试题详情
试题详情
试题详情
A.2 B.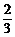 C.3 D.6 C.3 D.6 试题详情
4.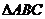 中,若 中,若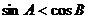 ,则 ,则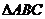 为 ( ) 为 ( ) A.锐角三角形
B.直角三角形 C.钝角三角形 D.不能确定 试题详情
5. 若函数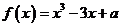 有3个不同的零点,则实数 有3个不同的零点,则实数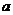 的取值范围是
( ) 的取值范围是
( ) 试题详情
试题详情
6.若不等式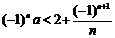 对于任意正整数n恒成立,则实数a的取值范围是 ( ) 对于任意正整数n恒成立,则实数a的取值范围是 ( ) 试题详情
试题详情
二.填空题:把答案填在答题卡相应题号后的横线上(本大题共3小题,每小题5分,共15分) 7.已知函数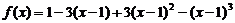 ,则 ,则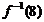 =
. =
. 试题详情
8. 某校高三级有三位数学老师,为便于学生询问,从星期一到星期五每天都安排数学教师值班,并且星期一安排两位老师值班,若每位老师每周值班两天,则一周内安排值班的方案有 种. 试题详情
试题详情
三.解答题:解答应写出文字说明,证明过程或演算步骤(本大题共3小题,共43分)
试题详情
已知各项都不相等的等差数列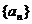 的前六项和为60,且 的前六项和为60,且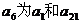 的等比中项. 的等比中项. 试题详情
(I)求数列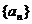 的通项公式 的通项公式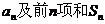 ; ; 试题详情
(II)若数列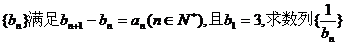 的前n项和Tn . 的前n项和Tn . 试题详情
试题详情
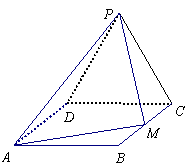 如图,边长为2的等边△PCD所在的平面垂直于矩形ABCD所在的平面,BC= 如图,边长为2的等边△PCD所在的平面垂直于矩形ABCD所在的平面,BC=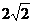 ,M为BC的中点 ,M为BC的中点
(Ⅰ)证明:AM⊥PM ; (Ⅱ)求二面角P-AM-D的大小; 试题详情
(Ⅲ)求点D到平面AMP的距离 试题详情
试题详情
试题详情
(Ⅰ) 求椭圆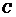 的方程; 的方程; 试题详情
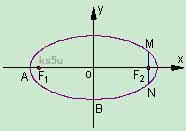 (Ⅱ) 设椭圆 (Ⅱ) 设椭圆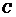 的左顶点为A,下顶点为B,动点P满足 的左顶点为A,下顶点为B,动点P满足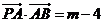 ,( ,(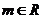 )试求点P的轨迹方程,使点B关于该轨迹的对称点落在椭圆 )试求点P的轨迹方程,使点B关于该轨迹的对称点落在椭圆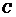 上. 上. 
试题详情
一. 选择题(本大题共6小题,每小题7分,共42分) 题号 1 2 3 4 5 6 答案 C B C C A A 二. 填空题(本大题共3小题,每小题5分,共15分) 7. 0
8. 36
9.  三.解答题:解答应写出文字说明,证明过程或演算步骤(本大题共3小题,共43分) 10.(本小题满分14分) 解:(I)设等差数列 的公差为 的公差为 ,则 ,则  …………2分 …………2分 解得 …………4分 …………4分  . …………5分 . …………5分  …………7分 …………7分 (II)由   …………10分 …………10分  …………12分 …………12分  
 …………14分 …………14分 11.(本小题满分14分) 解法1:(Ⅰ) 取CD的中点E,连结PE、EM、EA. ∵△PCD为正三角形,∴PE⊥CD,PE=PDsin∠PDE=2sin60°= ∵平面PCD⊥平面ABCD,
∴PE⊥平面ABCD
(2分) ∵四边形ABCD是矩形 ∴△ADE、△ECM、△ABM均为直角三角形 由勾股定理可求得:EM= ,AM= ,AM= ,AE=3 ,AE=3 ∴ (4分)
(4分)  ,又 ,又 在平面ABCD上射影: 在平面ABCD上射影:
∴∠AME=90°, ∴AM⊥PM
(6分) (Ⅱ)由(Ⅰ)可知EM⊥AM,PM⊥AM ∴∠PME是二面角P-AM-D的平面角
(8分) ∴tan ∠PME= ∴∠PME=45° ∴二面角P-AM-D为45°;
(10分) (Ⅲ)设D点到平面PAM的距离为 ,连结DM,则 ,连结DM,则  , ∴ , ∴
而 (12分)
(12分) 在 中,由勾股定理可求得PM= 中,由勾股定理可求得PM=   ,所以: ,所以: ∴ ∴ 
即点D到平面PAM的距离为  (14分)
(14分) 解法2:(Ⅰ) 以D点为原点,分别以直线DA、DC为x轴、y轴,建立如图所示的空间直角坐标系 , , 依题意,可得    ……2分 ……2分
∴  (4分) (4分)
∴ 即 ,∴AM⊥PM ,∴AM⊥PM (6分)
(6分) (Ⅱ)设 ,且 ,且 平面PAM,则 平面PAM,则  即
即
∴ , ,  取 ,得 ,得 (8分)
(8分) 取 ,显然 ,显然 平面ABCD, ∴ 平面ABCD, ∴ 结合图形可知,二面角P-AM-D为45°; (10分) (Ⅲ) 设点D到平面PAM的距离为 ,由(Ⅱ)可知 ,由(Ⅱ)可知 与平面PAM垂直,则 与平面PAM垂直,则  = = 
即点D到平面PAM的距离为  (14分)
(14分) 12.(本小题满分15分) 解:(Ⅰ)∵ 轴,∴ 轴,∴ ,由椭圆的定义得: ,由椭圆的定义得: (2分) (2分) ∵ ,∴ ,∴ ,
(4分) ,
(4分) 又 得 得 ∴ ∴   ∴ ,
(6分) ,
(6分) ∴所求椭圆C的方程为 .
(7分) .
(7分) (Ⅱ)由(Ⅰ)知点A(-2,0),点B为(0,-1),设点P的坐标为 则 , , , , 由 -4得- -4得- , , ∴点P的轨迹方程为 .
(9分) .
(9分) 设点B关于P的轨迹的对称点为 ,则由轴对称的性质可得: ,则由轴对称的性质可得:  ,解得: ,解得: ,
(12分) ,
(12分)
∵点 在椭圆上,∴ 在椭圆上,∴
 , , 整理得 解得 解得 或 或
 ∴点P的轨迹方程为 或 或 ,
(14分) ,
(14分) 经检验 和 和 都符合题设, 都符合题设, ∴满足条件的点P的轨迹方程为 或 或 .
(15分) .
(15分)
| 