
2006-2007学年度东营市利津县第二学期期中考试
初三数学试题
一、选择题 (3分×12=36分)
1、在Rt△ABC,∠C=90°, ,则tanA等于 ( )
,则tanA等于 ( )
A、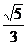 B、
B、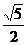 C、
C、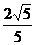 D、
D、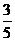
2、函数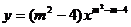 是一个二次函数,则
是一个二次函数,则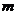 的值为 ( )
的值为 ( )
A、3 B、-2 C、-3或2 D、3或-2
3、抛物线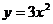 ,
,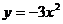 ,
,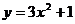 共有的一条性质是 ( )
共有的一条性质是 ( )
A、它们的顶点坐标相同 B、开口方向相同
C、 随
随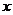 的增大而增大 D、对称轴相同
的增大而增大 D、对称轴相同
4、在△ABC中,∠A、∠B都是锐角,且 ,则△ABC的形状是 ( )
,则△ABC的形状是 ( )
A、直角三角形 B、锐角三角形 C、钝角三角形 D、不能确定
5、二次函数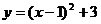 的图像顶点坐标是 ( )
的图像顶点坐标是 ( )
A、(-1,3) B、(1,3) C、(-1,-3) D、(1,-3)
6、若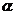 、
、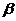 是锐角,且
是锐角,且 ,则下列正确的是 ( )
,则下列正确的是 ( )
A、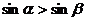 B、
B、 C、
C、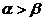 D、
D、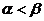
7、下列函数中,与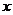 轴只有一个公共点的是 ( )
轴只有一个公共点的是 ( )
A、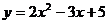 B、
B、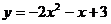
C、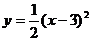 D、
D、
8、将进货单价为50元的某商品按零售价80元售出,每天可卖出20个,若在一定范围内每降1元,日销量增加1个,为了获取最大日销售利润,则应降价 ( )
A、5元 B、10元 C、15元 D、20元
9、函数 与
与 的图像可能是 ( )
的图像可能是 ( )

10、等腰三角形底边长是
A、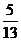 B、
B、 C、
C、 D、
D、
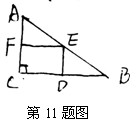
11、在Rt△ABC中,∠C=90°AC=30,BC=40,使内接矩形CDEF面积最大则EF的长是 ( )
A、l0 B、
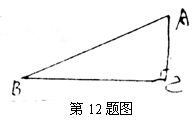
12、在Rt△ABC中,∠C=90°,∠ABC=15°,BC=1,则AC的长为 ( )
A、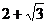 B、
B、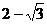 C、0.3 D、
C、0.3 D、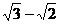
二、填空题(4分×5=20分)
13、在△ABC中,∠A=30,tanB= ,BC=
,BC=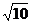 ,则AB=___________。
,则AB=___________。
14、将一抛物线向左平移2个单位,又向上平移3个单位得抛物线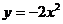 ,则原抛物线解析式是______________________。
,则原抛物线解析式是______________________。
15、函数 图像过点(-l,0),则
图像过点(-l,0),则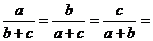 ___________。
___________。
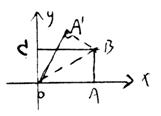
16、如图在直角坐标系中,将矩形OABC沿OB对折,点A落在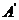 处,已知OA=
处,已知OA= ,AB=1,则
,AB=1,则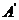 的坐标是___________。
的坐标是___________。
17、△ABC中,∠A=30°,AB=6,AC=4,则 ___________。
___________。
三、解答题
18、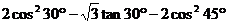 (8分)
(8分)
19、若一抛物线顶点坐标为(-2,3)且过点(0,I),求其解折式。 (8分)
20、下面左图为一楼房楼梯的侧截面图,原设计坡角∠ABC为40°,后考虑到安全标准,将坡角减至∠ADC=36°,若楼梯高2米,问楼梯多占地长多少长? (10分)

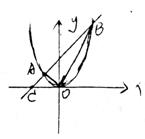
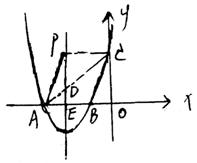
21、已知抛物线 与直线
与直线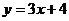 交于A、B两点,直线
交于A、B两点,直线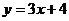 交
交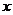 轴于点C。如上面右图所示
轴于点C。如上面右图所示
①求A、B坐标及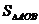 。
。
②抛物线上是否存在点D,使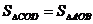 ,若存在求出D坐标,若不存在请说明理由? (12分)
,若存在求出D坐标,若不存在请说明理由? (12分)
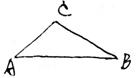
22、一船自西向东航行,在A处测得航标C在北偏东61°方向上,前进100米到达B处,又测得航标C在偏东45°方向上,在以航标C为圆心,120米为半径的圆形区域内有暗礁,如果船继续前行,有没有触礁危险。( ) (12分)
) (12分)

23、已知抛物线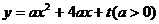 交
交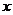 轴于A、B两点,交
轴于A、B两点,交 轴于C点,抛物线对称轴交
轴于C点,抛物线对称轴交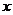 轴于E点,点B坐标为(-1,0) (14分)
轴于E点,点B坐标为(-1,0) (14分)
①求抛物线对称轴及A点坐标。 (4分)
②过点C作CP∥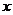 轴交对称轴于P,判断四边形ABCP是什么四边形并证明。 (5分)
轴交对称轴于P,判断四边形ABCP是什么四边形并证明。 (5分)
③连结CA与抛物线对称轴交于点D,若么,∠APD=∠ACP,求抛物线解析式。(5分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com