
2009年浙江省初中毕业生学业考试(湖州市)
数学试卷
卷Ⅰ
一、选择题(本题有12小题,每小题3分,共36分)
1.下列各数中,最大的数是
A.一l
B.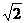
2.4的算术平方根是
A.2 B.一
3.如图是由4个大小相同的小立方块搭成的几何体,其主视图是

4.已知一粒大米的质量为0.000
A.0.21×10―4 B.2.1×10―
5.如图,在Rt△ABC中,∠ACB=90°,BC=1,AB=2,则下列结论正确的是

A. B.
B.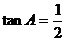 C.cosB=
C.cosB=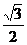 D.
D.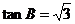
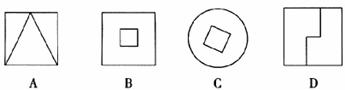
6.下列图形中,不是中心对称图形的是
7.已知⊙O1与⊙O2外切,它们的半径分别是2和3,则圆心距O1O2的长是
A.O1O2=1 B.O1O2=5 C.1< O1O2<5 D.O1O2>5
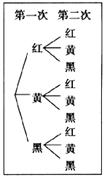
8.在一个布袋中装着只有颜色不同,其他都相同的红、黄、黑三种小球各一个,从中任意摸出一个球,记下颜色后放回并搅匀,再摸出一个球,两次摸球所有可能的结果如图所示,则摸出的两个球中,一个是红球,一个是黑球的概率是
A.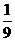 B.
B.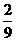 C.
C.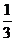 D.
D.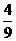
9.某商场用加权平均数来确定什锦糖的单价.由单价为15元/千克的甲种糖果
A.11元/千克 B.11.5元/千克 C.12元/千克 D.12.5元/千克
10.如图,一只蚂蚁从O点出发,沿着扇形OAB的边缘匀速爬行一周,设蚂蚁的运动时间为t,蚂蚁到O点的距离为s,则s关于t的函数图象大致为
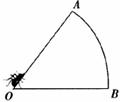
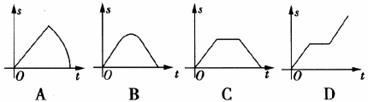
11.如图,在正三角形ABC中,D、E、F分别是BC、AC、AB上的点,DE⊥AC,EF⊥AB,FD⊥BC,则△DEF的面积与△ABC的面积之比等于
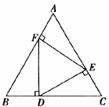
A.1:3 B.2: :2 D.
:2 D. :3
:3
12.已知图中的每个小方格都是边长为1的小正方形,每个小正方形的顶点称为格点,请你在图中任意画一条抛物线,问所画的抛物线最多能经过81个格点中的多少个?

A.6 B.7 C.8 D.9
卷Ⅱ
二、填空题(本题有6小题,每小题4分,共24分)
13.计算:|一3|一2=_________.
14.分解因式: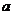 3―4
3―4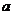 =________.
=________.
15.如图,已知在Rt△ABC中,∠ACB=90°,AB=4,分别以AC、BC为直径作半圆,面积分别为S1、S2,则S1+S2的值等于________.

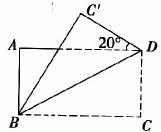
16.如图,已知矩形ABCD,将△BCD沿对角线BD折叠,记点C的对应点为C’.若∠ADC’=20°,则∠BDC的度数为________.
17.已知抛物线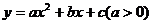 的对称轴为直线
的对称轴为直线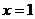 ,且经过点(-1,y1),(2,y2),试比较y1和y2的大小:y1_______y2(填“>”,“<”或“=”).
,且经过点(-1,y1),(2,y2),试比较y1和y2的大小:y1_______y2(填“>”,“<”或“=”).
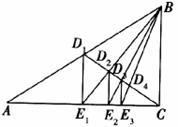
18.如图,已知Rt△ABC,D1是斜边AB的中点,过D1作D1E1⊥AC于E1,连接BEl交CDl于D2;过D2作D2E2⊥AC于E2,连接BE2交CDl于D3;过D3作D3E3⊥AC于E3,……如此继续,可以依次得到点D4,D5,…,Dn,分别记△BD1E1,△BD2E2,△BD3E3,…,△BDnEn的面积为S1、S2、S3,……Sn,则Sn=____________S△ABC(用含n的代数式表示)
三、解答题(本题有6小题,共60分)
19.(本题有2小题,每小题5分,共10分)
(1)计算:2cos60°一(2
009一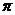 )0+
)0+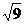 .
.
(2)解方程: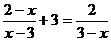
20.(本小题8分)如图,已知在△ABC中,AB=AC,D为BC边的中点,过点D作DE⊥AB,DF⊥AC,垂足分别为E、F
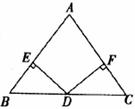
(1)求证:△BED≌△CFD;
(2)若∠A=90°,求证:四边形DFAE是正方形.
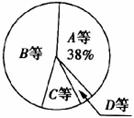
21.(本小题10分)某校为了解九年级男生l 000米长跑的成绩,从中随机抽取了50名男生进行测试,根据测试评分标准,将他们的得分进行统计后分为A,B,C,D四等,并绘制成下面的频数分布表和扇形统计图.
等第
成绩(得分)
频数(人数)
频率
A
10分
7
0.14
9分
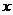
m
B
8分
15
0.30
7分
8
0.16
C
6分
4
0.08
5分
y
n
D
5分以下
3
0.06
合计
50
1.00
(1)试直接写出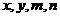 的值;
的值;
(2)求表示得分为C等的扇形的圆心角的度数;
(3)如果该校九年级共有男生200名,试估计这200名男生中成绩达到A等和B等的人数共有多少人?
22.(本小题10分)随着人民生活水平的不断提高,我市家庭轿车的拥有量逐年增加.据统计,某小区2006年底拥有家庭轿车64辆,2008年底家庭轿车的拥有量达到100辆.
(1)若该小区2006年底到2009年底家庭轿车拥有量的年平均增长率都相同,求该小区到2009年底家庭轿车将达到多少辆?
(2)为了缓解停车矛盾,该小区决定投资l5万元再建造若干停车位.据测算,建造费用分别为室内车位5 000元/个,露天车位1 000元/个,考虑到实际因素,计划露天车位的数量不少于室内车位的2倍,但不超过室内车位的2.5倍,求该小区最多可建两种车位各多少个?试写出所有可能的方案.
23.(本小题10分)如图,在平面直角坐标系中,直线 :
: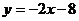 分别与
分别与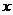 轴,y轴相交于A,B两点,点P(0,k)是y轴的负半轴上的一个动点,以P为圆心,3为半径作⊙P.
轴,y轴相交于A,B两点,点P(0,k)是y轴的负半轴上的一个动点,以P为圆心,3为半径作⊙P.
(1)连接PA,若PA=PB,试判断⊙P与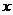 轴的位置关系,并说明理由;
轴的位置关系,并说明理由;
(2)当k为何值时,以⊙P与直线 的两个交点和圆心P为顶点的三角形是正三角形?
的两个交点和圆心P为顶点的三角形是正三角形?
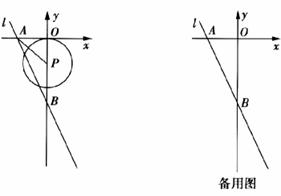
24.(本小题12分)已知:抛物线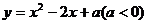 与y轴相交于点A,顶点为A.直线
与y轴相交于点A,顶点为A.直线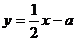 分别与
分别与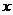 轴,y轴相交于B,C两点,并且与直线AM相交于点N.
轴,y轴相交于B,C两点,并且与直线AM相交于点N.
(1)填空:试用含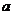 的代数式分别表示点M与N的坐标,则M(____,____),N(____,____).
的代数式分别表示点M与N的坐标,则M(____,____),N(____,____).
(2)如图,将△NAC沿y轴翻折,若点N的对应点N’恰好落在抛物线上,AN’与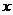 轴交于点D,连接CD,求
轴交于点D,连接CD,求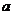 的值和四边形ADCN的面积.
的值和四边形ADCN的面积.
(3)在抛物线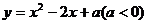 上是否存在一点P,使得以P,A,C,N为顶点的四边形是平行四边形?若存在,求出P点的坐标:若不存在,试说明理由.
上是否存在一点P,使得以P,A,C,N为顶点的四边形是平行四边形?若存在,求出P点的坐标:若不存在,试说明理由.

请注意:本题为自选题,供考生选做.自选题得分将计入本学科总分,但考试总分最多为120分。
四、自选题(本题5分)
25.若P为△ABC所在平面上一点,且∠APB=∠BPC=∠CPA=120°,则点P叫做△ABC的费马点.
(1)若点P为锐角三角形ABC的费马点,且∠ABC=60°,PA=3,PC=4,则PB的值为_____;
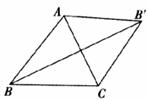
(2)如图,在锐角三角形ABC外侧作等边三角形ACB’,连接BB’.
求证:BB’过△ABC的费马点P,且BB’=PA+PB+PC.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com