
假期复习第十二天―――三角函数的图象和性质
一.这几个概念你掌握了吗?请回顾一遍:
1.正弦、余弦函数的图象的画法, “五点法”画正弦、余弦函数和函数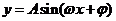 的简图。
的简图。
2. 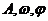 的物理意义,由函数
的物理意义,由函数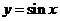 的图象到函数
的图象到函数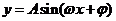 的图象的变换原理.
的图象的变换原理.
3.三角函数的定义域、值域、周期的求法
4.三角函数奇偶性的判断及三角函数单调区间的求解。
二.特别要注意下列方法:
1.“五点法”画正弦、余弦函数和函数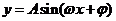 的简图,五个特殊点通常都是取三个平衡点,一个最高、一个最低点;
的简图,五个特殊点通常都是取三个平衡点,一个最高、一个最低点;
2.给出图象求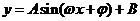 的解析式的难点在于
的解析式的难点在于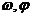 的确定,本质为待定系数法,基本方法是:①寻找特殊点(平衡点、最值点)代入解析式;②图象变换法,即考察已知图象可由哪个函数的图象经过变换得到的,通常可由平衡点或最值点确定周期
的确定,本质为待定系数法,基本方法是:①寻找特殊点(平衡点、最值点)代入解析式;②图象变换法,即考察已知图象可由哪个函数的图象经过变换得到的,通常可由平衡点或最值点确定周期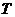 ,进而确定
,进而确定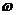 .
.
3.求三角函数的值域的常用方法:①化为求代数函数的值域;②化为求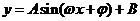 的值域;③化为关于
的值域;③化为关于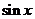 (或
(或 )的二次函数式;
)的二次函数式;
4.三角函数的周期问题一般将函数式化为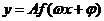 (其中
(其中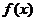 为三角函数,
为三角函数,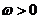 ).
).
5.函数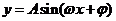
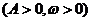 的单调区间的确定,基本思路是把
的单调区间的确定,基本思路是把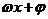 看作一个整体,运用复合函数的单调规律得解;
看作一个整体,运用复合函数的单调规律得解;
三.下列习题你必须掌握:
1.将函数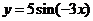 的周期扩大到原来的2倍,再将函数图象左移
的周期扩大到原来的2倍,再将函数图象左移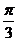 ,得到图象对应解析式是
,得到图象对应解析式是
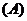
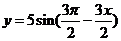
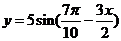
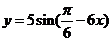
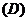
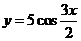
2.若函数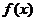 图象上每一个点的纵坐标保持不变,横坐标伸长到原来的两倍,然后再将整个图象沿
图象上每一个点的纵坐标保持不变,横坐标伸长到原来的两倍,然后再将整个图象沿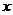 轴向右平移
轴向右平移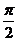 个单位,向下平移3个单位,恰好得到
个单位,向下平移3个单位,恰好得到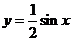 的图象,则
的图象,则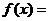 .
.
3.先将函数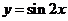 的图象向右平移
的图象向右平移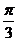 个单位长度,再将所得图象作关于
个单位长度,再将所得图象作关于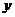 轴的对称变换,则所得函数图象对应解析式为 .
轴的对称变换,则所得函数图象对应解析式为 .
4.函数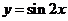 的图象向右平移
的图象向右平移 (
(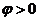 )个单位,得到的图象关于直线
)个单位,得到的图象关于直线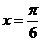 对称,则
对称,则 的最小值为
的最小值为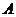
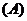
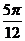
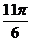
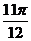
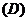 以上都不对
以上都不对
 5.已知函数
5.已知函数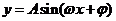
(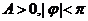 )的一段图象如
)的一段图象如
下图所示,求函数的解析式.
6.求函数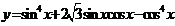 的最小正周期和最小值;并写出该函数在
的最小正周期和最小值;并写出该函数在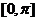 上的单调递增区间。
上的单调递增区间。
7.求值域:(1)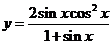 ;(2)
;(2)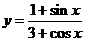 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com