科目：gzsx 来源：同步题 题型：单选题
科目：gzsx 来源： 题型：
cosπx),b=(1,sinπx),令f(x)=a·b. (1)求函数f(x)的最小正周期;
(2)若函数y=f(x+φ)的图象关于原点对称,求满足该条件的φ的最小正值.
科目：gzsx 来源： 题型：013
已知函数y = f (x)，(f (x)不恒等于0 )与y =-f (x)的图象关于原点对称，则y = f (x)
[
]A
．是奇函数而不是偶函数 B．是偶函数而不是奇函数C
．是奇函数也是偶函数 D．不是奇函数也不是偶函数科目：gzsx 来源： 题型：
（1）y=f(x)的图象关于原点对称
（2）y=f(x)为周期函数且最小正周期是4
（3）y=f(x)在区间［2，4］上是减函数
正确命题的个数为
A.0 B.1 C.2 D.3
科目：gzsx 来源： 题型：单选题
科目：gzsx 来源：河南省郑州市2010届高中毕业年级第三次质量预测文科数学试题 题型：044
定义在R上的函数f(x)＝ax3＋bx2＋cx＋d满足：函数f(x)的图象关于原点对称且过点(3，－6)，函数f(x)在点x1、x2处取得极值，且|x1－x2|＝4．
(Ⅰ)求函数f(x)的表达式；
(Ⅱ)求函数f(x)的单调区间；
(Ⅲ)求函数f(x)过点P(1，－8)的切线方程．
科目：gzsx 来源： 题型：
| 1 | 3-x |
科目：gzsx 来源： 题型：
| 1 |
| 2-x |
| A、y=10x |
| B、y=10x-2 |
| C、y=lgx |
| D、y=lg（x-2） |
科目：gzsx 来源： 题型：
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 4 |
| 3 |
| 4 |
| 1 |
| 2 |
| 5 |
| 4 |
科目：gzsx 来源： 题型：
| 1 |
| 1-x |
科目：gzsx 来源：不详 题型：填空题
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 4 |
| 3 |
| 4 |
| 1 |
| 2 |
| 5 |
| 4 |
科目：gzsx 来源：不详 题型：单选题
| 1 |
| 1-x |
| A．y=10x | B．y=10x-1 | C．y=lgx | D．y=lg（x-1） |
科目：gzsx 来源：2012-2013学年浙江省宁波市余姚中学高一（上）期中数学试卷（理科）（解析版） 题型：填空题
； 
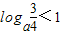则a
；
]；
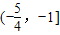． 科目：gzsx 来源： 题型：
(本小题满分16分)知函数f(x)＝ax3＋bx2＋cx＋d(a、b、c、d
R)，且函数f(x)的图象关于原点对称，其图象x＝3处的切线方程为8x－y－18＝0.
(1)求f(x)的解析式；
(2)是否存在区间
，使得函数f(x)的定义域和值域均为？若存在，求出这样的一个区间；若不存在，则说明理由；
(3)若数列｛an｝满足：a1≥1，an+1≥
，试比较＋＋＋…＋与1的大小关系，并说明理由.
科目：gzsx 来源： 题型：
已知函数f（x）=-
（a＞0且a≠1），
（1）证明：函数y=f(x)的图象关于点
对称；
（2）求f（-2）+f（-1）+f（0）+f（1）+f（2）+f（3）的值.
科目：gzsx 来源： 题型：022
关于函数
有下列命题：
(1)
可得
必定是p
的整数倍；
(2)
y=f(x)的表达式可改写成
；
(3)
y=f(x)的图象关于点
对称．其中正确的命题序号是______． 科目：gzsx 来源：2008届山东省潍坊市高三教学质量检测数学试卷(文科) 题型：044
已知函数f(x)＝ax2＋2x＋b的图象过点(1，3)，且f(－1＋x)＝f(－1－x)对任意实数x都成立，函数y＝g(x)与y＝f(x)的图象关于原点对称．
(1)求f(x)与g(x)的解析式；
(2)若F(x)＝g(x)－λf(x)在[－1，1]上是增函数，求实数λ的取值范围．
．试求f(x)在R上的表达式，并画出它的图象，根据图象写出它的单调区间？
．试求f(x)在R上的表达式，并画出它的图象，根据图象写出它的单调区间？